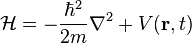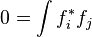Eigenfunction

In mathematics, an eigenfunction of a linear operator, A, defined on some function space, is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has
for some scalar, λ, the corresponding eigenvalue. The solution of the differential eigenvalue problem also depends on any boundary conditions required of  . In each case there are only certain eigenvalues
. In each case there are only certain eigenvalues  (
( ) that admit a corresponding solution for
) that admit a corresponding solution for 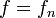 (with each
(with each  belonging to the eigenvalue
belonging to the eigenvalue  ) when combined with the boundary conditions. Eigenfunctions are used to analyze
) when combined with the boundary conditions. Eigenfunctions are used to analyze  .
.
For example, 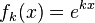 is an eigenfunction for the differential operator
is an eigenfunction for the differential operator
for any value of  , with corresponding eigenvalue
, with corresponding eigenvalue  . If boundary conditions are applied to this system (e.g.,
. If boundary conditions are applied to this system (e.g.,  at two physical locations in space), then only certain values of
at two physical locations in space), then only certain values of 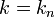 satisfy the boundary conditions, generating corresponding discrete eigenvalues
satisfy the boundary conditions, generating corresponding discrete eigenvalues  .
.
Specifically, in the study of signals and systems, the eigenfunction of a system is the signal 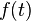 which when input into the system, produces a response
which when input into the system, produces a response  with the complex constant
with the complex constant 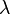 .[1]
.[1]
Examples
Derivative operator
A widely used class of linear operators acting on function spaces are the differential operators on function spaces. As an example, on the space  of infinitely differentiable real functions of a real argument
of infinitely differentiable real functions of a real argument  , the process of differentiation is a linear operator since
, the process of differentiation is a linear operator since
for any functions  and
and 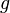 in
in  , and any real numbers
, and any real numbers  and
and  .
.
The eigenvalue equation for a linear differential operator  in
in  is then a differential equation
is then a differential equation
The functions that satisfy this equation are commonly called eigenfunctions. For the derivative operator  , an eigenfunction is a function that, when differentiated, yields a constant times the original function. That is,
, an eigenfunction is a function that, when differentiated, yields a constant times the original function. That is,
for all  . This equation can be solved for any value of
. This equation can be solved for any value of 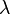 . The solution is an exponential function
. The solution is an exponential function
The derivative operator is defined also for complex-valued functions of a complex argument. In the complex version of the space  , the eigenvalue equation has a solution for any complex constant
, the eigenvalue equation has a solution for any complex constant 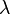 . The spectrum of the operator
. The spectrum of the operator  is therefore the whole complex plane. This is an example of a continuous spectrum.
is therefore the whole complex plane. This is an example of a continuous spectrum.
Applications
Vibrating strings

Let  denote the sideways displacement of a stressed elastic chord, such as the vibrating strings of a string instrument, as a function of the position
denote the sideways displacement of a stressed elastic chord, such as the vibrating strings of a string instrument, as a function of the position  along the string and of time
along the string and of time  . From the laws of mechanics, applied to infinitesimal portions of the string, one can deduce that the function
. From the laws of mechanics, applied to infinitesimal portions of the string, one can deduce that the function  satisfies the partial differential equation
satisfies the partial differential equation
which is called the (one-dimensional) wave equation. Here  is a constant that depends on the tension and mass of the string.
is a constant that depends on the tension and mass of the string.
This problem is amenable to the method of separation of variables. If we assume that  can be written as the product of the form
can be written as the product of the form  , we can form a pair of ordinary differential equations:
, we can form a pair of ordinary differential equations:
-
 and
and 
Each of these is an eigenvalue equation, for eigenvalues  and
and  , respectively. For any values of
, respectively. For any values of 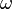 and
and  , the equations are satisfied by the functions
, the equations are satisfied by the functions
-
 and
and 
where  and
and  are arbitrary real constants. If we impose boundary conditions (that the ends of the string are fixed with
are arbitrary real constants. If we impose boundary conditions (that the ends of the string are fixed with  at
at  and
and  , for example) we can constrain the eigenvalues. For those boundary conditions, we find
, for example) we can constrain the eigenvalues. For those boundary conditions, we find
-
 , and so the phase angle
, and so the phase angle 
and
Thus, the constant 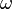 is constrained to take one of the values
is constrained to take one of the values  , where
, where  is any integer. Thus, the clamped string supports a family of standing waves of the form
is any integer. Thus, the clamped string supports a family of standing waves of the form
From the point of view of our musical instrument, the frequency  is the frequency of the
is the frequency of the  th harmonic, which is called the
th harmonic, which is called the  th overtone.
th overtone.
Quantum mechanics
Eigenfunctions play an important role in many branches of physics. An important example is quantum mechanics, where the Schrödinger equation
 ,
,
with
has solutions of the form
where 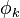 are eigenfunctions of the operator
are eigenfunctions of the operator  with eigenvalues
with eigenvalues  . The fact that only certain eigenvalues
. The fact that only certain eigenvalues  with associated eigenfunctions
with associated eigenfunctions 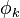 satisfy Schrödinger's equation leads to a natural basis for quantum mechanics and the periodic table of the elements, with each
satisfy Schrödinger's equation leads to a natural basis for quantum mechanics and the periodic table of the elements, with each  an allowable energy state of the system. The success of this equation in explaining the spectral characteristics of hydrogen is considered one of the greatest triumphs of 20th century physics.
an allowable energy state of the system. The success of this equation in explaining the spectral characteristics of hydrogen is considered one of the greatest triumphs of 20th century physics.
Due to the nature of Hermitian Operators such as the Hamiltonian operator  , its eigenfunctions are orthogonal functions. This is not necessarily the case for eigenfunctions of other operators (such as the example
, its eigenfunctions are orthogonal functions. This is not necessarily the case for eigenfunctions of other operators (such as the example  mentioned above). Orthogonal functions
mentioned above). Orthogonal functions  ,
,  have the property that
have the property that
where  is the complex conjugate of
is the complex conjugate of 
whenever  , in which case the set
, in which case the set  is said to be orthogonal. Also, it is linearly independent.
is said to be orthogonal. Also, it is linearly independent.
Notes
- ↑ Bernd Girod, Rudolf Rabenstein, Alexander Stenger, Signals and systems, 2nd ed., Wiley, 2001, ISBN 0-471-98800-6 p. 49
References
- Methods of Mathematical Physics by R. Courant, D. Hilbert ISBN 0-471-50447-5 (Volume 1 Paperback) ISBN 0-471-50439-4 (Volume 2 Paperback) ISBN 0-471-17990-6 (Hardback)
See also
- Eigenvalue, eigenvector and eigenspace
- Hilbert–Schmidt theorem
- Spectral theory of ordinary differential equations
- Fixed point combinator
- More images (non-GPL) at Atom in a Box