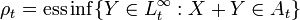Dynamic risk measure

From Wikipedia, the free encyclopedia

In financial mathematics, a conditional risk measure is a random variable of the financial risk (particularly the downside risk) as if measured at some point in the future. A risk measure can be thought of as a conditional risk measure on the trivial sigma algebra.

A dynamic risk measure is a risk measure that deals with the question of how evaluations of risk at different times are related. It can be interpreted as a sequence of conditional risk measures. ^[1]

Conditional risk measure

A mapping 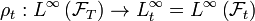$\rho _{t}:L^{{\infty }}\left({\mathcal {F}}_{T}\right)\rightarrow L_{t}^{{\infty }}=L^{{\infty }}\left({\mathcal {F}}_{t}\right)$ is a conditional risk measure if it has the following properties:

Conditional cash invariance: $\forall m_{t}\in L_{t}^{{\infty }}:\;\rho _{t}(X+m_{t})=\rho _{t}(X)-m_{t}$

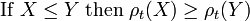
Monotonicity: ${\mathrm {If}}\;X\leq Y\;{\mathrm {then}}\;\rho _{t}(X)\geq \rho _{t}(Y)$

Normalization: $\rho _{t}(0)=0$

If it is a conditional convex risk measure then it will also have the property:

Conditional convexity: $\forall \lambda \in L_{t}^{{\infty }},0\leq \lambda \leq 1:\rho _{t}(\lambda X+(1-\lambda )Y)\leq \lambda \rho _{t}(X)+(1-\lambda )\rho _{t}(Y)$

A conditional coherent risk measure is a conditional convex risk measure that additionally satisfies:

Conditional positive homogeneity: $\forall \lambda \in L_{t}^{{\infty }},\lambda \geq 0:\rho _{t}(\lambda X)=\lambda \rho _{t}(X)$

Acceptance set

Main article: Acceptance set

The acceptance set at time 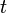$t$ associated with a conditional risk measure is

$A_{t}=\{X\in L_{T}^{{\infty }}:\rho (X)\leq 0{\text{ a.s.}}\}$ .

If you are given an acceptance set at time 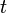$t$ then the corresponding conditional risk measure is

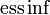$\rho _{t}={\text{ess}}\inf\{Y\in L_{t}^{{\infty }}:X+Y\in A_{t}\}$

where ${\text{ess}}\inf$ is the essential infimum.^[2]

Regular property

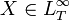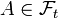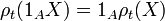A conditional risk measure $\rho _{t}$ is said to be regular if for any $X\in L_{T}^{{\infty }}$ and $A\in {\mathcal {F}}_{t}$ then $\rho _{t}(1_{A}X)=1_{A}\rho _{t}(X)$ where $1_{A}$ is the indicator function on $A$ . Any normalized conditional convex risk measure is regular.^[3]

The financial interpretation of this states that the conditional risk at some future node (i.e. $\rho _{t}(X)[\omega ]$ ) only depends on the possible states from that node. In a binomial model this would be akin to calculating the risk on the subtree branching off from the point in question.

Time consistent property

Main article: Time consistency

A dynamic risk measure is time consistent if and only if 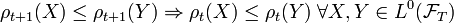$\rho _{{t+1}}(X)\leq \rho _{{t+1}}(Y)\Rightarrow \rho _{t}(X)\leq \rho _{t}(Y)\;\forall X,Y\in L^{{0}}({\mathcal {F}}_{T})$ .^[4]

Example: dynamic superhedging price

The dynamic superhedging price has conditional risk measures of the form: $\rho _{t}(-X)=\operatorname *{ess\sup }_{{Q\in EMM}}{\mathbb {E}}^{Q}[X|{\mathcal {F}}_{t}]$ . It is a widely shown result that this is also a time consistent risk measure.

References

↑ Acciaio, Beatrice; Penner, Irina (February 22, 2010). Dynamic risk measures (pdf). Retrieved July 22, 2010.
↑ Penner, Irina (2007). Dynamic convex risk measures: time consistency, prudence, and sustainability (pdf). Retrieved February 3, 2011.
↑ Detlefsen, K.; Scandolo, G. (2005). "Conditional and dynamic convex risk measures". Finance and Stochastics 9 (4): 539–561.
↑ Cheridito, Patrick; Stadje, Mitja (October 2008). Time-inconsistency of VaR and time-consistent alternatives.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.