Duoprism

From Wikipedia, the free encyclopedia
Set of uniform p,q-duoprisms
TypePrismatic uniform polychoron
Schläfli symbol{p}×{q}
Coxeter-Dynkin diagram
Cellsp q-gonal prisms,
q p-gonal prisms
Facespq squares,
p q-gons,
q p-gons
Edges2pq
Verticespq
Vertex figure
disphenoid
Symmetry[p,2,q], order 4pq
Dualp,q-duopyramid
Propertiesconvex, vertex-uniform
 
Set of uniform p,p-duoprisms
TypePrismatic uniform polychoron
Schläfli symbol{p}×{p}
Coxeter-Dynkin diagram
Cells2p p-gonal prisms
Facesp2 squares,
2p p-gons
Edges2p2
Verticesp2
Symmetry[[p,2,p]], order 8p2
Dualp,p-duopyramid
Propertiesconvex, vertex-uniform, Facet-transitive
A close up inside the 23-29 duoprism projected onto a 3-sphere, and perspective projected to 3-space. As m and n become large, a duoprism approaches the geometry of duocylinder just like a p-gonal prism approaches a cylinder.

In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an n-polytope and an m-polytope is an (n+m)-polytope, where n and m are 2 (polygon) or higher.

The lowest dimensional duoprisms exist in 4-dimensional space as polychora (4-polytopes) being the Cartesian product of two polygons in 2-dimensional Euclidean space. More precisely, it is the set of points:

P_{1}\times P_{2}=\{(x,y,z,w)|(x,y)\in P_{1},(z,w)\in P_{2}\}

where P1 and P2 are the sets of the points contained in the respective polygons. Such a duoprism is convex if both bases are convex, and is bounded by prismatic cells.

Nomenclature

Four-dimensional duoprisms are considered to be prismatic polychora. A duoprism constructed from two regular polygons of the same size is a uniform duoprism.

A duoprism made of n-polygons and m-polygons is named by prefixing 'duoprism' with the names of the base polygons, for example: a triangular-pentagonal duoprism is the Cartesian product of a triangle and a pentagon.

An alternative, more concise way of specifying a particular duoprism is by prefixing with numbers denoting the base polygons, for example: 3,5-duoprism for the triangular-pentagonal duoprism.

Other alternative names:

  • q-gonal-p-gonal prism
  • q-gonal-p-gonal double prism
  • q-gonal-p-gonal hyperprism

The term duoprism is coined by George Olshevsky, shortened from double prism. Conway proposed a similar name proprism for product prism.

Example 16,16-duoprism

Schlegel diagram

Projection from the center of one 16-gonal prism, and all but one of the opposite 16-gonal prisms are shown.		 net

The two sets of 16-gonal prisms are shown. The top and bottom faces of the vertical cylinder are connected when folded together in 4D.

Geometry of 4-dimensional duoprisms

A 4-dimensional uniform duoprism is created by the product of a regular n-sided polygon and a regular m-sided polygon with the same edge length. It is bounded by n m-gonal prisms and m n-gonal prisms. For example, the Cartesian product of a triangle and a hexagon is a duoprism bounded by 6 triangular prisms and 3 hexagonal prisms.

  • When m and n are identical, the resulting duoprism is bounded by 2n identical n-gonal prisms. For example, the Cartesian product of two triangles is a duoprism bounded by 6 triangular prisms.
  • When m and n are identically 4, the resulting duoprism is bounded by 8 square prisms (cubes), and is identical to the tesseract.

The m-gonal prisms are attached to each other via their m-gonal faces, and form a closed loop. Similarly, the n-gonal prisms are attached to each other via their n-gonal faces, and form a second loop perpendicular to the first. These two loops are attached to each other via their square faces, and are mutually perpendicular.

As m and n approach infinity, the corresponding duoprisms approach the duocylinder. As such, duoprisms are useful as non-quadric approximations of the duocylinder.

Images of uniform polychoral duoprisms

All of these images are Schlegel diagrams with one cell shown. The p-q duoprisms are identical to the q-p duoprisms, but look different because they are projected in the center of different cells.

6-prism 6-6-duoprism
A hexagonal prism, projected into the plane by perspective, centered on a hexagonal face, looks like a double hexagon connected by (distorted) squares. Similarly a 6-6 duoprism projected into 3D approximates a torus, hexagonal both in plan and in section.

3-3
(triddip)
3-4
(tisdip)
3-5
(trapedip)
3-6
(thiddip)
3-7
(theddip)
3-8
(todip)

4-3
(tisdip)
4-4
(tes)
4-5
(squipdip)
4-6
(shiddip)
4-7
(shedip)
4-8
(sodip)

5-3
(trapedip)
5-4
(squipdip)
5-5
(pedip)
5-6
(phiddip)
5-7
(pheddip)
5-8
(podip)

6-3
(thiddip)
6-4
(shiddip)
6-5
(phiddip)
6-6
(hiddip)
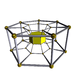6-7
(hahedip)
6-8
(hodip)

7-3
(theddip)
7-4
(shedip)
7-5
(pheddip)
7-6
(hahedip)
7-7
(hedip)
7-8
(heodip)

8-3
(todip)
8-4
(sodip)
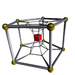8-5
(podip)
8-6
(hodip)
8-7
(heodip)
8-8
(odip)

Related polytopes

The regular skew polyhedron, {4,4|n}, exists in 4-space as the n2 square faces of a n-n duoprism, using all 2n2 edges and n2 vertices. The 2n n-gonal faces can be seen as removed. (skew polyhedra can be seen in the same way by a n-m duoprism, but these are not regular.)

Duoantiprism

p-q duoantiprism vertex figure, a gyrobifastigium

Like the antiprisms as alternated prisms, there is a set of 4-dimensional duoantiprisms polychora that can be created by an alternation operation applied to a duoprism. The alternated vertices create nonregular tetrahedral cells, except for the special case, the 4-4 duoprism (tesseract) which creates the uniform (and regular) 16-cell. The 16-cell is the only convex uniform duoantiprism.

See also grand antiprism.

The duoprisms , t0,1,2,3{p,2,q}, can be alternated into , ht0,1,2,3{p,2,q}, the "duoantiprisms", which cannot be made uniform in general. The only convex uniform solution is the trivial case of p=q=2, which is a lower symmetry construction of the tesseract , t0,1,2,3{2,2,2}, with its alternation as the 16-cell, , ht0,1,2,3{2,2,2}.

The only nonconvex uniform solution is p=5, q=5/3, ht0,1,2,3{5,2,5/3}, , constructed from 10 pentagonal antiprisms, 10 pentagrammic crossed-antiprisms, and 50 tetrahedra, known as the great duoantiprism (gudap).[1][2]

k_22 polytopes

The 3-3 duoprism, -122, is first in a dimensional series of uniform polytopes, expressed by Coxeter as k22 series. The 3-3 duoprism is the vertex figure for the second, the birectified 5-simplex. The fourth figure is a Euclidean honeycomb, 222, and the final is a noncompact hyperbolic honeycomb, 322. Each progressive uniform polytope is constructed from the previous as its vertex figure.

k22 figures in n dimensions
n 4 5 6 7 8
Coxeter
group		 A22 A5 E6 Failed to parse(Cannot store math image on filesystem.): {{\tilde {E}}}_{{6}}=E6+ E6++
Coxeter
diagram
Symmetry
(order)		 [[32,2,-1]]
(72)		 [[32,2,0]]
(1440)		 [[32,2,1]]
(103,680)		 [[32,2,2]]
(∞)		 [[32,2,3]]
(∞)
Graph ∞ ∞
Name −122 022 122 222 322

See also

Notes

  1. ↑ Jonathan Bowers - Miscellaneous Uniform Polychora 965. Gudap
  2. ↑ http://www.polychora.com/12GudapsMovie.gif Animation of cross sections

References

External links

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.