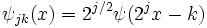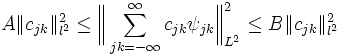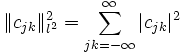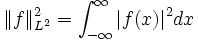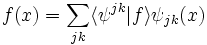Dual wavelet
In mathematics, a dual wavelet is the dual to a wavelet. In general, the wavelet series generated by a square integrable function will have a dual series, in the sense of the Riesz representation theorem. However, the dual series is not in general representable by a square integral function itself.
Definition
Given a square integrable function  , define the series
, define the series  by
by
for integers 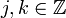 .
.
Such a function is called an R-function if the linear span of  is dense in
is dense in  , and if there exist positive constants A, B with
, and if there exist positive constants A, B with 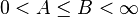 such that
such that
for all bi-infinite square summable series 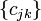 . Here,
. Here, 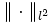 denotes the square-sum norm:
denotes the square-sum norm:
and  denotes the usual norm on
denotes the usual norm on  :
:
By the Riesz representation theorem, there exists a unique dual basis 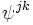 such that
such that
where  is the Kronecker delta and
is the Kronecker delta and  is the usual inner product on
is the usual inner product on  . Indeed, there exists a unique series representation for a square integrable function f expressed in this basis:
. Indeed, there exists a unique series representation for a square integrable function f expressed in this basis:
If there exists a function 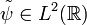 such that
such that
then  is called the dual wavelet or the wavelet dual to ψ. In general, for some given R-function ψ, the dual will not exist. In the special case of
is called the dual wavelet or the wavelet dual to ψ. In general, for some given R-function ψ, the dual will not exist. In the special case of  , the wavelet is said to be an orthogonal wavelet.
, the wavelet is said to be an orthogonal wavelet.
An example of an R-function without a dual is easy to construct. Let  be an orthogonal wavelet. Then define
be an orthogonal wavelet. Then define  for some complex number z. It is straightforward to show that this ψ does not have a wavelet dual.
for some complex number z. It is straightforward to show that this ψ does not have a wavelet dual.
See also
References
- Charles K. Chui, An Introduction to Wavelets (Wavelet Analysis & Its Applications), (1992), Academic Press, San Diego, ISBN 0-12-174584-8