Dual-beta
In investing, dual-beta is a concept that states that a regular, market beta can be divided into downside beta and upside beta. Thus, dual stands for two betas, upside and downside. The fundamental principle behind dual-beta is that upside and downside betas are not the same. This is in contrast to what the Capital Asset Pricing Model assumes, which is that upside and downside betas are identical.[1]:617 Moreover, Fama and French (1992) demonstrated that beta is an imperfect measure of investment risk.[2]
Formula
The dual-beta model allows investors to differentiate downside risk – risk of loss – from upside risk, or gain. Regular beta fails to acknowledge, and thus to permit, this distinction. The dual-beta model does not assume that upside beta and downside betas are the same but actually calculates what the values are for the two betas, thus allowing investors to make better-informed investing decisions. “The dual-beta model can thus be expressed as:
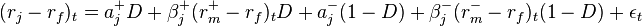
where the dependent variable,  is the “the asset return in excess of the riskless rate, the two intercepts are
is the “the asset return in excess of the riskless rate, the two intercepts are  and
and  , for the ‘up-market’ and ‘down-market’ regime respectively, and
, for the ‘up-market’ and ‘down-market’ regime respectively, and 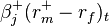 is the product of the ‘up-market beta’ and the up-market excess return, and similarly
is the product of the ‘up-market beta’ and the up-market excess return, and similarly  is the product of the ‘down-market beta’ and the down-market excess return.[3]:348
is the product of the ‘down-market beta’ and the down-market excess return.[3]:348  ,
,  ,
,  , and
, and 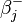 are the estimated parameters for up-market and down-market days, respectively;
are the estimated parameters for up-market and down-market days, respectively;  on days the market index did not decline and
on days the market index did not decline and  on days it did;
on days it did;  is a dummy variable, which takes the value of 1 when the market index daily return is non-negative and zero otherwise.”[1]:618 “The final term,
is a dummy variable, which takes the value of 1 when the market index daily return is non-negative and zero otherwise.”[1]:618 “The final term,  , reflects the idiosyncratic information not proportional to either the up-market or down-market excess returns.”[3]:348
, reflects the idiosyncratic information not proportional to either the up-market or down-market excess returns.”[3]:348
Dual-Beta vs. Beta
Dual-beta can be a useful and an effective extension to traditional beta, which “underestimates equity risk about half the time, compared with the dual-beta estimate…which can translate into large differences in present value computations.”[3]:345 The dual-beta model is particularly useful because CAPM beta “consistently lags the dual-betas, in terms of average daily returns and return-to-standard deviation ratio.”[4]:71 Thus, investors can use the dual-beta approach to minimize their downside risk and maximize their upside risk/gain which cannot be achieved through the use of standard beta and the standard CAPM. While there the dual-beta model has many benefits in terms of accuracy and usefulness, it might not be cost-effective for individual investors and is more suitable for financial planners due to transaction costs.[4]:80-81
See also
- Beta
- Capital asset pricing model
- Cost of capital
- Downside beta
- Downside risk
- Financial risk
- Macro risk
- Upside beta
- Upside risk
References
- ↑ 1.0 1.1 Chong, James; Halcoussis, Dennis; Phillips, Michael G. (September–October 2012). "Misleading Betas: An Educational Example". American Journal Of Business Education 5 (5). Retrieved 26 June 2013.
- ↑ Fama, Eugene F.; French, Kenneth (1992). "The Cross-Section of Expected Stock Returns". Journal of Finance 47 (2): 427–465. doi:10.2307/2329112.
- ↑ 3.0 3.1 3.2 Chong, James; Phillips, Michael G. (December 14, 2011). "Measuring risk for cost of capital: The downside beta approach". Journal of Corporate Treasury Management 4 (4). Retrieved 26 June 2013.
- ↑ 4.0 4.1 Chong, James, Ph.D.; Pfeiffer, Shaun, Ph.D.; Phillips, Michael G., Ph.D. (2011). "Can Dual Beta Filtering Improve Investor Performance". Journal of Personal Finance 10 (1). Retrieved 26 June 2013.
External links
- MacroRisk Analytics "Patented and proprietary macro risk measurements and tools for investors since 1999".
- DualBeta
- Zacks "Zacks Investment Research: Stock Research, Analysis, & Recommendations".
- A Study of Sharpe's asymmetric beta model
- Rethinking Valuation and Pricing Models, 1st Edition
- Capital Asset Pricing Model Calculator