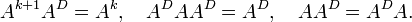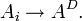Drazin inverse

From Wikipedia, the free encyclopedia

In mathematics, the Drazin inverse, named after Michael P. Drazin, is a kind of generalized inverse of a matrix.

Let A be a square matrix. The index of A is the least nonnegative integer k such that rank(A^k+1) = rank(A^k). The Drazin inverse of A is the unique matrix A^D which satisfies

$A^{{k+1}}A^{D}=A^{k},\quad A^{D}AA^{D}=A^{D},\quad AA^{D}=A^{D}A.$

If A is invertible with inverse $A^{{-1}}$ , then $A^{D}=A^{{-1}}$ .

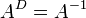The Drazin inverse of a matrix of index 0 or 1 is called the group inverse or {1,2,5}-inverse and denoted A^#. The group inverse can be defined, equivalently, by the properties AA^#A = A, A^#AA^# = A^#, and AA^# = A^#A.

A projection matrix P, defined as a matrix such that P² = P, has index 1 (or 0) and has Drazin inverse P^D = P.

If A is a nilpotent matrix (for example a shift matrix), then $A^{D}=0.$

The hyper-power sequence is

$A_{{i+1}}:=A_{i}+A_{i}\left(I-AA_{i}\right);$ for convergence notice that $A_{{i+j}}=A_{i}\sum _{{k=0}}^{{2^{j}-1}}(I-AA_{i})^{k}.$

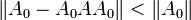For $A_{0}:=\alpha A$ or any regular $A_{0}$ with $A_{0}A=AA_{0}$ chosen such that $\|A_{0}-A_{0}AA_{0}\|<\|A_{0}\|$ the sequence tends to its Drazin inverse,

$A_{i}\rightarrow A^{D}.$

References

Drazin, M. P., (1958). "Pseudo-inverses in associative rings and semigroups". The American Mathematical Monthly 65 (7): 506–514. doi:10.2307/2308576. JSTOR 2308576.

Zheng, Bing; Bapat, R.B (2004). "Generalized inverse A(2)T,S and a rank equation". Applied Mathematics and Computation 155 (2): 407. doi:10.1016/S0096-3003(03)00786-0.

External links

Drazin inverse on Planet Math
Group inverse on Planet Math

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Drazin inverse

See also

References

External links