DrGeo
| Original author(s) | Hilaire Fernandes |
|---|---|
| Initial release | December 31, 1996 |
| Stable release | 11.12 / December 10, 2011 |
| Development status | Active |
| Written in | Pharo |
| Operating system | Linux, Mac OS X, Windows |
| Type | Interactive geometry software |
| License | GPL |
| Website | www.drgeo.eu |
DrGeo is a free (under GNU GPL license) software, created by Hilaire Fernandes for the Ofset. As its names suggests, it is a geometry software. It runs over GTK+ interface.
Objects
Points
DrGeo has two kinds of points: A free one, which can be moved with the mouse (but may be attached to a curve), and a point given by its coordinates.
There is also the intersection of 2 curves and the midpoint of a segment.
Lines
DrGeo is equipped with the classic line, ray, segment and vector.
There are also the circle (defined by 2 points) but also the less classic arc by three points. DrGeo can also construct polygons (given by points) and loci.
Transformations
Besides the parallel and perpendicular line through a point, DrGeo can apply to a point one of these transformations:
- reflexion
- symmetry
- translation
- rotation
- homothety
Macros
When some objects, called final depend from other objects, called initial it is possible to create a new transformation sending the initial objects to the final ones. This is a macro. It allows to add new objects to DrGeo like regular polygons or new transformations like circle inversion.
Scripting
DrGeo comes up with a script language, which is Scheme (a Lisp-like language).
Scheme object
It is possible also to create a Guile object, which is a number, but created with a script, written in the Scheme syntax. It can have one or several variables, which are chosen at the creation of the object, with mouse clicks. The names of the variables are a1, a2 etc. For example, if one wants the square of a number a1, the script
(define x (getValue a1)) (* x x)
creates a numeric object, whose value is the square of the first number. If now the first number is changed, the second one changes too.
If now one wants to implement the square of a complex number, one has to create 2 numeric values, one for the real part, and the other one for the imaginary part. As 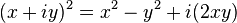 , the script for the real part is (once one has selected a free point)
, the script for the real part is (once one has selected a free point)
(define x (car (getCoordinates a1))) (define y (cadr (getCoordinates a1))) (- (* x x) (* y y))
and the script for the imaginary part (with the same point selected):
(define x (car (getCoordinates a1))) (define y (cadr (getCoordinates a1))) (* 2 x y)
getCoordinates a1 yields a list because a1 is a point, which has 2 coordinates. The CAR of this list is the first coordinate, which is the abscissa, and the CADR of the list (the CAR of the CDR) is the second coordinate.
Once this is done, it remains only to create a point which coordinates are the two numbers created by scripts, and a transformation is defined; it implements the function 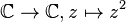 and can be transformed into a macro.
and can be transformed into a macro.
Scheme-generated figure
The Guile object can only create one number, then if one wants to create a complex figure by a script, one has to write the script with a text editor, save it with the scm file extension, then make DrGeo evaluate the file.
Here is how DrGeo can create a Sierpinski triangle recursively:
(new-figure "Sierpinski") (define (sierpin p1 p2 p3 n) (let* ( (p4 (Point "" milieu-2pts p2 p1)) (p5 (Point "" milieu-2pts p2 p3)) (p6 (Point "" milieu-2pts p3 p1)) (q1 (Polygone "" npoints p1 p4 p6)) (q2 (Polygone "" npoints p2 p4 p5)) (q3 (Polygone "" npoints p3 p5 p6))) (if (> n 1) (begin (envoi q1 masquer) (envoi q2 masquer) (envoi q3 masquer))) (envoi p4 masquer) (envoi p5 masquer) (envoi p6 masquer) (if (> n 0) (begin (sierpin p1 p4 p6 (- n 1)) (sierpin p2 p4 p5 (- n 1)) (sierpin p3 p5 p6 (- n 1)))))) (soit Point "A" free -3 -1) (soit Point "B" free 3 -1) (soit Point "C" free 0 3) (sierpin A B C 5)
See also
- Compass and straightedge construction
- Interactive geometry software