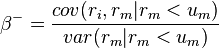Downside beta

From Wikipedia, the free encyclopedia

In investing, downside beta is the element of beta that investors associate with risk. It is defined to be the scaled amount by which an asset moves compared to a benchmark, calculated only on days when the benchmark’s return is negative.[1]

Formula

Downside beta measures downside risk. The CAPM can be modified to use semi-variance instead of standard deviation to measure risk.[2]

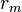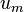Where r_{i} and r_{m} are the excess returns to security i and market m, and u_{m} is the average market excess return, the CAPM can be modified to incorporate downside (or upside) beta as follows,[3]

\beta ^{-}={\frac {cov(r_{i},r_{m}|r_{m}<u_{m})}{var(r_{m}|r_{m}<u_{m})}}

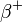Therefore, \beta ^{-} and \beta ^{+} can be estimated with a regression of excess return of security i on excess return of the market, conditional on excess market return being below the mean for downside beta (or above the mean for upside beta).[1] Downside beta is calculated from data points of the asset or portfolio return using only those days when the benchmark return is negative. Downside beta and upside beta are also differentiated in the dual-beta model.

Downside Beta vs. Beta

Downside beta is an effective measure of the risk-return relationship in both developed and growing markets. When companies are grouped according to their two-digit SIC codes, average downside beta is different from standard beta even at the industry average level. Downside market risk can also explain the systematic relative differences in value stocks versus growth stocks, which the CAPM has failed to do, especially in international markets.[4]

Downside beta has greater explanatory power than standard beta in bearish markets.[1][5] Portfolios that are constructed by minimizing downside beta may be able to maintain more of their value during times of market decline.

See also

References

  1. ↑ 1.0 1.1 1.2 Trent, William A. (1 May 2005). "Traditional Beta, Downside Risk Beta, and Market Risk Premiums". CFA Digest. CFA Institute. pp. 44–45. doi:10.2469/dig.v35.n2.1669. Retrieved 7 January 2014. 
  2. ↑ Hogan, W.W.; Warren, J.M. (1977). "Toward the development of an equilibrium capital-market model based on semi-variance". Journal of Financial and Quantitative Analysis 9 (1): 1–11. 
  3. ↑ Bawa, V.; Lindenberg, E. (1977). "Capital market equilibrium in a mean-lower partial moment framework". Journal of Financial Economics 5: 189–200. 
  4. ↑ Galsband, Victoria (16 October 2012). "Downside risk and the value anomaly". VoxEU.org. VOX. Retrieved 7 January 2014. 
  5. ↑ Estrada (2007). "Mean-semivariance behavior: Downside risk and capital asset pricing". International Review of Economics and Finance 16: 169.  Estrada computed standard betas and downside betas for stocks across 23 developed markets and 27 emerging markets. This research showed that downside beta did a better job of explaining variations of cross-section returns in both types of market than did standard beta. In emerging markets, downside beta explained 55% of variations in mean returns.

External links


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.