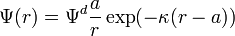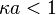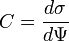Double layer (interfacial)
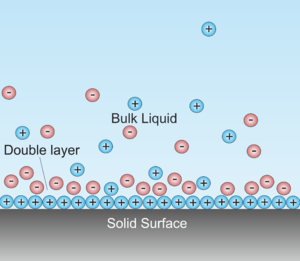
A double layer (DL, also called an electrical double layer, EDL) is a structure that appears on the surface of an object when it is exposed to a fluid. The object might be a solid particle, a gas bubble, a liquid droplet, or a porous body. The DL refers to two parallel layers of charge surrounding the object. The first layer, the surface charge (either positive or negative), comprises ions adsorbed onto the object due to chemical interactions. The second layer is composed of ions attracted to the surface charge via the coulomb force, electrically screening the first layer. This second layer is loosely associated with the object. It is made of free ions that move in the fluid under the influence of electric attraction and thermal motion rather than being firmly anchored. It is thus called the "diffuse layer".
Interfacial DL is most apparent in systems with a large surface area to volume ratio, such as colloid or porous bodies with particles or pores (respectively) on the scale of micrometres to nanometres. However, DL is important to other phenomena, such as the electrochemical behavior of electrodes.
The DL plays a fundamental role in many everyday substances. For instance, milk exists only because fat droplets are covered with a DL that prevent their coagulation into butter. DLs exist in practically all heterogeneous fluid-based systems, such as blood, paint, ink and ceramic and cement slurry.
The DL is closely related to electrokinetic phenomena and electroacoustic phenomena.
Development of the double layer model
Helmholtz

When a electronic conductor is brought in contact with a solid or liquid ionic conductor (electrolyte), a common boundary (interface) among the two phases appears. Hermann von Helmholtz [1] was the first to realize that charged electrodes immersed in electrolytic solutions repel the coions of the charge while attracting counterions to their surfaces. Two layers of opposite polarity form at the interface between electrode and electrolyte. In 1853 he showed that an electrical double layer (DL) that is essentially a molecular dielectric stored charge electrostatically.[2] Below the electrolyte's decomposition voltage the stored charge is linearly dependent on the voltage applied.
This early model predicted a constant differential capacitance independent from the charge density depending on the dielectric constant of the electrolyte solvent and the thickness of the double-layer.[3][4][5]
This model, while a good foundation for the description of the interface, does not consider important factors including diffusion/mixing of ions in solution, the possibility of adsorption onto the surface and the interaction between solvent dipole moments and the electrode.
Gouy-Chapman
Louis Georges Gouy in 1910 and David Leonard Chapman in 1913 both observed that capacitance was not a constant and that it depended on the applied potential and the ionic concentration. The "Gouy-Chapman model" made significant improvements by introducing a diffuse model of the DL. In this model the charge distribution of ions as a function of distance from the metal surface allows Maxwell–Boltzmann statistics to be applied. Thus the electric potential decreases exponentially away from the surface of the fluid bulk.[3][6]
Stern
Gouy-Chapman fails for highly charged DLs. In 1924 Otto Stern suggested combining Helmholtz with Gouy-Chapman. In Stern's model, some ions adhere to the electrode as suggested by Helmholtz, giving an internal Stern layer, while some form a Gouy-Chapman diffuse layer.[7]
The Stern layer accounted for ions' finite size and consequently ions' closest approach to the electrode is on the order of the ionic radius. The Stern model had its own limitations, effectively modeling ions as point charges, assuming all significant interactions in the diffuse layer are Coulombic, assuming dielectric permittivity to be constant throughout the double layer and that fluid viscosity is constant above the slipping plane.[8]
Grahame
_NT.PNG)
D. C. Grahame modified Stern in 1947.[9] He proposed that some ionic or uncharged species can penetrate the Stern layer, although the closest approach to the electrode is normally occupied by solvent molecules. This could occur if ions lose their solvation shell as they approach the electrode. He called ions in direct contact with the electrode "specifically adsorbed ions". This model proposed the existence of three regions. The inner Helmholtz plane (IHP) plane passes through the centres of the specifically adsorbed ions. The outer Helmholtz plane (OHP) passes through the centres of solvated ions at the distance of their closest approach to the electrode. Finally the diffuse layer is the region beyond the OHP.
Bockris/Devanthan/Müller
In 1963 J. O'M. Bockris, M. A. V. Devanthan and K. Alex Müller[10] proposed the BDM model of the double-layer that included the action of the solvent in the interface. They suggested that the attached molecules of the solvent, such as water, would have a fixed alignment to the electrode surface. This first layer of solvent molecules displays a strong orientation to the electric field depending on the charge. This orientation has great influence on the permittivity of the solvent that varies with field strength. The IHP passes through the centers of these molecules. Specifically adsorbed, partially solvated ions appear in this layer. The solvated ions of the electrolyte are outside the IHP. Through the centers of these ions pass the OHP. The diffuse layer is the region beyond the OHP. The BDM model now is most commonly used.
Trasatti/Buzzanca
Further research with double layers on ruthenium dioxide films in 1971 by Sergio Trasatti and Giovanni Buzzanca demonstrated that the electrochemical behavior of these electrodes at low voltages with specific adsorbed ions was like that of capacitors. The specific adsorption of the ions in this region of potential could also involve a partial charge transfer between the ion and the electrode. It was the first step towards understanding pseudocapacitance.[4]
Conway

Between 1975 and 1980 Brian Evans Conway conducted extensive fundamental and development work on ruthenium oxide electrochemical capacitors. In 1991 he described the difference between ‘Supercapacitor’ and ‘Battery’ behavior in electrochemical energy storage. In 1999 he coined the term supercapacitor to explain the increased capacitance by surface redox reactions with faradaic charge transfer between electrodes and ions.[11][12]
His "supercapacitor" stored electrical charge partially in the Helmholtz double-layer and partially as the result of faradaic reactions with "pseudocapacitance" charge transfer of electrons and protons between electrode and electrolyte. The working mechanisms of pseudocapacitors are redox reactions, intercalation and electrosorption.
Marcus
The physical and mathematical basics of electron charge transfer absent chemical bonds leading to pseudocapacitance was developed by Rudolph A. Marcus. Marcus Theory explains the rates of electron transfer reactions—the rate at which an electron can move from one chemical species to another. It was originally formulated to address outer sphere electron transfer reactions, in which two chemical species change only in their charge, with an electron jumping. For redox reactions without making or breaking bonds, Marcus theory takes the place of Henry Eyring's transition state theory which was derived for reactions with structural changes. Marcus received the Nobel Prize in Chemistry in 1992 for this theory.[citation needed]
Mathematical description
There are detailed descriptions of the interfacial DL in many books on colloid and interface science[13][14][15] and microscale fluid transport.[16][17] There is also a recent IUPAC technical report [18] on the subject of interfacial double layer and related electrokinetic phenomena.

As stated by Lyklema, "...the reason for the formation of a “relaxed” (“equilibrium”) double layer is the non-electric affinity of charge-determining ions for a surface..."[19] This process leads to the build up of an electric surface charge, expressed usually in C/m2. This surface charge creates an electrostatic field that then affects the ions in the bulk of the liquid. This electrostatic field, in combination with the thermal motion of the ions, creates a counter charge, and thus screens the electric surface charge. The net electric charge in this screening diffuse layer is equal in magnitude to the net surface charge, but has the opposite polarity. As a result the complete structure is electrically neutral.
The diffuse layer, or at least part of it, can move under the influence of tangential stress. There is a conventionally introduced slipping plane that separates mobile fluid from fluid that remains attached to the surface. Electric potential at this plane is called electrokinetic potential or zeta potential. It is also denoted as ζ-potential.
The electric potential on the external boundary of the Stern layer versus the bulk electrolyte is referred to as Stern potential. Electric potential difference between the fluid bulk and the surface is called the electric surface potential.
Usually zeta potential is used for estimating the degree of DL charge. A characteristic value of this electric potential in the DL is 25 mV with a maximum value around 100 mV (up to several volts on electrodes[17][20]). The chemical composition of the sample at which the ζ-potential is 0 is called the point of zero charge or the iso-electric point. It is usually determined by the solution pH value, since protons and hydroxyl ions are the charge-determining ions for most surfaces.[19][17]
Zeta potential can be measured using electrophoresis, electroacoustic phenomena, streaming potential, and electroosmotic flow.
The characteristic thickness of the DL is the Debye length, κ−1. It is reciprocally proportional to the square root of the ion concentration C. In aqueous solutions it is typically on the scale of a few nanometers and the thickness decreases with increasing concentration of the electrolyte.
The electric field strength inside the DL can be anywhere from zero to over 109 V/m. These steep electric potential gradients are the reason for the importance of the DLs.
The theory for a flat surface and a symmetrical electrolyte[19] is usually referred to as the Gouy-Chapman theory. It yields a simple relationship between electric charge in the diffuse layer σd and the Stern potential Ψd:
There is no general analytical solution for mixed electrolytes, curved surfaces or even spherical particles. There is an asymptotic solution for spherical particles with low charged DLs. In the case when electric potential over DL is less than 25 mV, the so-called Debye-Huckel approximation holds. It yields the following expression for electric potential Ψ in the spherical DL as a function of the distance r from the particle center:
There are several asymptotic models which play important roles in theoretical developments associated with the interfacial DL.
The first one is "thin DL". This model assumes that DL is much thinner than the colloidal particle or capillary radius. This restricts the value of the Debye length and particle radius as following:
This model offers tremendous simplifications for many subsequent applications. Theory of electrophoresis is just one example.[21] The theory of electroacoustic phenomena is another example.[22]
The thin DL model is valid for most aqueous systems because the Debye length is only a few nanometers in such cases. It breaks down only for nano-colloids in solution with ionic strengths close to water.
The opposing "thick DL" model assumes that the Debye length is larger than particle radius:
This model can be useful for some nano-colloids and non-polar fluids, where the Debye length is much larger.
The last model introduces "overlapped DLs".[22] This is important in concentrated dispersions and emulsions when distances between particles become comparable with the Debye length.
Electrical double layers
The electrical double layer (EDL) is a structure which describes the variation of electric potential near a surface, and has a significant influence on the behaviour of colloids and other surfaces in contact with solutions or solid-state fast ion conductors.
The primary difference between a DL on an electrode and one on an interface is the mechanisms of surface charge formation. With an electrode, it is possible to regulate the surface charge by applying an external electric potential. This application, however, is impossible in colloidal and porous DLs, because for colloidal particles, one does not have access to the interior of the particle to apply a potential difference.
EDLs are analogous to the double layer in plasma.
Differential capacitance
EDLs have an additional parameter defining their characterization: differential capacitance. Differential capacitance, denoted as C, is described by the equation below:
where σ is the surface charge and ψ is the electric surface potential.
See also
| Wikimedia Commons has media related to Electrical double layer. |
- Depletion region (structure of semiconductor junction)
- Electroosmotic pump
- Interface and colloid science
- Nanofluidics
- Supercapacitor
References
- ↑ H. Helmholtz (1853), "Ueber einige Gesetze der Vertheilung elektrischer Ströme in körperlichen Leitern mit Anwendung auf die thierisch-elektrischen Versuche" (in German), Annalen der Physik und Chemie 165 (6): pp. 211–233, doi:10.1002/andp.18531650603
- ↑ "The electrical double layer". 2011. Retrieved 23 April 2013.
- ↑ 3.0 3.1 Adam Marcus Namisnyk. "A survey of electrochemical supercapacitor technolog". Retrieved 2012-12-10.
- ↑ 4.0 4.1 S. Srinivasan, Fuel Cells, From Fundamentals to Applications, Springer eBooks, 2006, ISBN 978-0-387-35402-6,CHAPTER 2, ELECTRODE/ELECTROLYTE INTERFACES: STRUCTURE AND KINETICS OF CHARGE TRANSFER (769 kB)
- ↑ Electrochemical Double-Layer Capacitors Using Carbon Nanotube Electrode Structures
- ↑ Ehrenstein, Gerald (2001). "Surface charge". Retrieved 30 May 2011.
- ↑ Stern, O. Z.Electrochem, 30, 508 (1924)
- ↑ SMIRNOV, Gerald (2011). "Electric Double Layer". Retrieved 23 April 2013.
- ↑ D. C. Grahame, Chem. Rev., 41 (1947) 441
- ↑ J. O'M. Bockris, M. A. V Devanthan, and K. Mueller, Proc. Roy. Soc, Ser. A. 274, 55 (1963)
- ↑ B. E. Conway (Mai 1991), "Transition from ‘Supercapacitor’ to ‘Battery’ Behavior in Electrochemical Energy Storage" (in German), Journal of The Electrochemical Society 138 (6): pp. 1539–1548, doi:10.1149/1.2085829
- ↑ A. K. Shukla, T. P. Kumar , Electrochemistry Encyclopedia, PILLARS OF MODERN ELECTROCHEMISTRY: A BRIEF HISTORY Central Electrochemical Research Institute, (November, 2008)
- ↑ Dukhin, S.S. & Derjaguin, B.V. "Electrokinetic Phenomena", J.Willey and Sons, 1974
- ↑ Russel, W.B., Saville, D.A. and Schowalter, W.R. “Colloidal Dispersions”, Cambridge University Press,1989
- ↑ Kruyt, H.R. “Colloid Science”, Elsevier: Volume 1, Irreversible systems, (1952)
- ↑ Bruus, H. (2007). Theoretical Microfluidics.
- ↑ 17.0 17.1 17.2 Kirby, B.J. (2010). Micro- and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices.. Cambridge University Press. ISBN 978-0-521-11903-0.
- ↑ ”Measurement and Interpretation of Electrokinetic Phenomena”, International Union of Pure and Applied Chemistry, Technical Report, published in Pure Appl.Chem., vol 77, 10, pp.1753-1805, 2005 (pdf)
- ↑ 19.0 19.1 19.2 Lyklema, J. “Fundamentals of Interface and Colloid Science”, vol.2, page.3.208, 1995
- ↑ V.S. Bogotsky, Fundamentals of Electrochemistry, Wiley-Interscience, 2006.
- ↑ Hunter, R.J. "Foundations of Colloid Science", Oxford University Press, 1989
- ↑ 22.0 22.1 Dukhin, A.S.; Goetz, P.J. (2002). "Electroacoustic Theory". Ultrasound for Characterizing Colloids. Elsevier. p. 33. Retrieved 2007-10-03.
External links
- The Electrical Double Layer
- Electrical double layer: revisit based on boundary conditions
- J Chem Phys