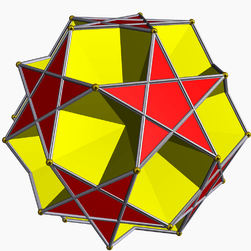
Dodecadodecahedron
| Dodecadodecahedron | |
|---|---|
 | |
| Type | Uniform star polyhedron |
| Elements | F = 24, E = 60 V = 30 (χ = −6) |
| Faces by sides | 12{5}+12{5/2} |
| Wythoff symbol(s) | 2 | 5 5/2 2 | 5 5/3 2 | 5/2 5/4 2 | 5/3 5/4 |
| Symmetry group | Ih, [5,3], *532 |
| Index references | U36, C45, W73 |
| Bowers acronym | Did |
 5.5/2.5.5/2 (Vertex figure) |
 Medial rhombic triacontahedron (dual polyhedron) |
In geometry, the dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U36.
Wythoff constructions
It has four Wythoff constructions between four Schwarz triangle families: 2 | 5 5/2, 2 | 5 5/3, 2 | 5/2 5/4, 2 | 5/3 5/4, but represent identical results. Similarly it can be given four extended Schläfli symbols: t1{5/2,5}, t1{5/3,5}, t1{5/2,5/4}, and t1{5/3,5/4}. And it can also be given four Coxeter-Dynkin diagrams: ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , and
, and ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Net
A shape with the same exterior appearance as the dodecadodecahedron can be constructed by folding up these nets:

12 pentagrams and 20 rhombic clusters are necessary. However, this construction replaces the crossing pentagonal faces of the dodecadodecahedron with non-crossing sets of rhombs, so it does not produce the same internal structure.
Related polyhedra
Its convex hull is the icosidodecahedron. It also shares its edge arrangement with the small dodecahemicosahedron (having the pentagrammic faces in common), and with the great dodecahemicosahedron (having the pentagonal faces in common).
 Dodecadodecahedron |
 Small dodecahemicosahedron |
 Great dodecahemicosahedron |
 Icosidodecahedron (convex hull) |
This polyhedron can be considered a rectified great dodecahedron. It is center of a truncation sequence between a small stellated dodecahedron and great dodecahedron:
The truncated small stellated dodecahedron looks like a dodecahedron on the surface, but it has 24 faces: 12 pentagons from the truncated vertices and 12 overlapping as (truncated pentagrams). The truncation of the dodecadodecahedron itself is not uniform, but it has a uniform quasitruncation, the truncated dodecadodecahedron.
| Name | Small stellated dodecahedron | Truncated small stellated dodecahedron | Dodecadodecahedron | Truncated great dodecahedron |
Great dodecahedron |
|---|---|---|---|---|---|
| Coxeter-Dynkin diagram |
|||||
| Picture |  |
 |
 |
 |
 |
It is topologically equivalent to a quotient space of the hyperbolic order-4 pentagonal tiling, by distorting the pentagrams back into regular pentagons. As such, it is topologically a regular polyhedron of index two:[1][2]

The colours in the above image correspond to the red pentagrams and yellow pentagons of the dodecadodecahedron at the top of this article.
See also
References
- ↑ The Regular Polyhedra (of index two), David A. Richter
- ↑ The Golay Code on the Dodecadodecahedron, David A. Richter
External links
| |||||||||||||||||