Distribution (differential geometry)

From Wikipedia, the free encyclopedia

In differential geometry, a discipline within mathematics, a distribution is a subset of the tangent bundle of a manifold satisfying certain properties. Distributions are used to build up notions of integrability, and specifically of a foliation of a manifold.

Even though they share the same name, distributions we discuss in this article have nothing to do with distributions in the sense of analysis.

Definition

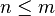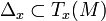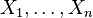Let $M$ be a $C^{\infty }$ manifold of dimension $m$ , and let $n\leq m$ . 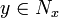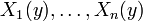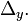Suppose that for each $x\in M$ , we assign an $n$ -dimensional subspace $\Delta _{x}\subset T_{x}(M)$ of the tangent space in such a way that for a neighbourhood $N_{x}\subset M$ of $x$ there exist $n$ linearly independent smooth vector fields $X_{1},\ldots ,X_{n}$ such that for any point $y\in N_{x}$ , $X_{1}(y),\ldots ,X_{n}(y)$ span $\Delta _{y}.$ We let $\Delta$ refer to the collection of all the $\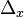Delta _{x}$ for all $x\in M$ and we then call $\Delta$ a distribution of dimension $n$ on $M$ , or sometimes a $C^{\infty }$ $n$ -plane distribution on 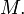$M.$ The set of smooth vector fields 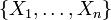$\{X_{1},\ldots ,X_{n}\}$ is called a local basis of $\Delta .$

Involutive distributions

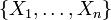We say that a distribution $\Delta$ on $M$ is involutive if for every point $x\in M$ there exists a local basis $\{X_{1},\ldots ,X_{n}\}$ of the distribution in a neighbourhood of $x$ such that for all $1\leq i,j\leq n$ , $[X_{i},X_{j}]$ (the Lie bracket of two vector fields) is in the span of $\{X_{1},\ldots ,X_{n}\}.$ That is, if $[X_{i},X_{j}]$ is a linear combination of $\{X_{1},\ldots ,X_{n}\}.$ Normally this is written as $[\Delta ,\Delta ]\subset \Delta .$

Involutive distributions are the tangent spaces to foliations. Involutive distributions are important in that they satisfy the conditions of the Frobenius theorem, and thus lead to integrable systems.

A related idea occurs in Hamiltonian mechanics: two functions f and g on a symplectic manifold are said to be in mutual involution if their Poisson bracket vanishes.

Generalized distributions

A generalized distribution, or Stefan-Sussmann distribution, is similar to a distribution, but the subspaces 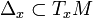$\Delta _{x}\subset T_{x}M$ are not required to all be of the same dimension. The definition requires that the 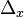$\Delta _{x}$ are determined locally by a set of vector fields, but these will no longer be linearly independent everywhere. It is not hard to see that the dimension of 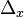$\Delta _{x}$ is lower semicontinuous, so that at special points the dimension is lower than at nearby points.

One class of examples is furnished by a non-free action of a Lie group on a manifold, the vector fields in question being the infinitesimal generators of the group action (a free action gives rise to a genuine distribution). Another arises in dynamical systems, where the set of vector fields in the definition is the set of vector fields that commute with a given one. There are also examples and applications in Control theory, where the generalized distribution represents infinitesimal constraints of the system.

References

William M. Boothby. Section IV. 8. Frobenius's Theorem in An Introduction to Differentiable Manifolds and Riemannian Geometry, Academic Press, San Diego, California, 2003.
P. Stefan, Accessible sets, orbits and foliations with singularities. Proc. London Math. Soc. 29 (1974), 699-713.
H.J. Sussmann, Orbits of families of vector fields and integrability of distributions. Trans. Amer. Math. Soc. 180 (1973), 171-188.

This article incorporates material from Distribution on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.