Distortion function
From Wikipedia, the free encyclopedia
A distortion function ![g:[0,1]\to [0,1]](/2014-wikipedia_en_all_02_2014/I/media/9/7/f/d/97fd26d67e9595db275d4a69efc1fd5b.png) is a non-decreasing function such that
is a non-decreasing function such that 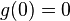 and
and  . The dual distortion function is
. The dual distortion function is 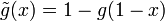 .[1][2] Distortion functions are used to define distortion risk measures.[2]
.[1][2] Distortion functions are used to define distortion risk measures.[2]
Given a probability space 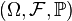 , then for any random variable
, then for any random variable  and any distortion function
and any distortion function 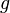 we can define a new probability measure
we can define a new probability measure  such that for any
such that for any 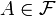 it follows that
it follows that
References
- ↑ 1.0 1.1 Balbás, A.; Garrido, J.; Mayoral, S. (2008). "Properties of Distortion Risk Measures". Methodology and Computing in Applied Probability 11 (3): 385. doi:10.1007/s11009-008-9089-z.
- ↑ 2.0 2.1 Julia L. Wirch; Mary R. Hardy. "Distortion Risk Measures: Coherence and Stochastic Dominance" (pdf). Retrieved March 10, 2012.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.
