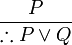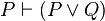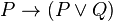Disjunction introduction

From Wikipedia, the free encyclopedia

Transformation rules
Propositional calculus
Rules of inference Modus ponens Modus tollens Biconditional introduction Biconditional elimination Conjunction introduction Simplification Disjunction introduction Disjunction elimination Disjunctive syllogism Hypothetical syllogism Constructive dilemma Destructive dilemma Absorption Rules of replacement Associativity Commutativity Distributivity Double negation De Morgan's laws Transposition Material implication Material equivalence Exportation Tautology
Predicate logic
Universal generalization Universal instantiation Existential generalization Existential instantiation
v t e

Disjunction introduction or addition^[1]^[2]^[3] is a simple valid argument form, an immediate inference and a rule of inference of propositional logic. The rule makes it possible to introduce disjunctions to logical proofs. It is the inference that if P is true, then P or Q must be true.

Socrates is a man.

Therefore, either Socrates is a man or pigs are flying in formation over the English Channel.

The rule can be expressed as:

${\frac {P}{\therefore P\lor Q}}$

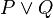where the rule is that whenever instances of " $P$ " appear on lines of a proof, " $P\lor Q$ " can be placed on a subsequent line.

Disjunction introduction is controversial in paraconsistent logic because in combination with other rules of logic, it leads to explosion (i.e. everything becomes provable). See Tradeoffs in Paraconsistent logic.

Formal notation

The disjunction introduction rule may be written in sequent notation:

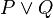$P\vdash (P\lor Q)$

where $\vdash$ is a metalogical symbol meaning that $P\lor Q$ is a syntactic consequence of $P$ in some logical system;

and expressed as a truth-functional tautology or theorem of propositional logic:

$P\to (P\lor Q)$

where $P$ and $Q$ are propositions expressed in some formal system.

References

↑ Hurley
↑ Moore and Parker
↑ Copi and Cohen

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.