Disjoint sets

From Wikipedia, the free encyclopedia
Two disjoint sets.

In mathematics, two sets are said to be disjoint if they have no element in common. Equivalently, disjoint sets are sets whose intersection is the empty set.[1] For example, {1, 2, 3} and {4, 5, 6} are disjoint sets.

Generalizations

This definition of disjoint sets can be extended to any family of sets. A family of sets is pairwise disjoint or mutually disjoint if every two different sets in the family are disjoint.[1] For example, the collection of sets { {1}, {2}, {3}, ... } is pairwise disjoint.

Almost disjoint sets are sets whose intersection is small in some sense. For instance, two infinite sets whose intersection is a finite set may be said to be almost disjoint.[2]

In topology, there are various notions of separated sets with more strict conditions than disjointness. For instance, two sets may be considered to be separated when they have disjoint closures or disjoint neighborhoods. Similarly, in a metric space, positively separated sets are sets separated by a nonzero distance.[3]

Intersections

Disjointness of two sets, or of a family of sets, may be expressed in terms of their intersections.

Two sets A and B are disjoint if and only if their intersection 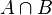A\cap B is the empty set.[1] It follows from this definition that every set is disjoint from the empty set, and that the empty set is the only set that is disjoint from itself.[4]

A family F of sets is pairwise disjoint if, for every two sets in the family, their intersection is empty.[1] If the family contains more than one set, this implies that the intersection of the whole family is also empty. However, a family of only one set is pairwise disjoint, regardless of whether that set is empty, and may have a non-empty intersection. Additionally, a family of sets may have an empty intersection without being pairwise disjoint.[5] For instance, the three sets { {1, 2}, {2, 3}, {1, 3} } have an empty intersection but are not pairwise disjoint. In fact, there are no two disjoint sets in this collection.

A Helly family is a system of sets within which the only subfamilies with empty intersections are the ones that are pairwise disjoint. For instance, the closed intervals of the real numbers form a Helly family: if a family of closed intervals has an empty intersection and is minimal (i.e. no subfamily of the family has an empty intersection), it must be pairwise disjoint.[6]

Disjoint unions and partitions

A partition of a set X is any collection of mutually disjoint non-empty sets whose union is X.[7] Every partition can equivalently be described by an equivalence relation, a binary relation that describes whether two elements belong to the same set in the partition.[7] Disjoint-set data structures[8] and partition refinement[9] are two techniques in computer science for efficiently maintaining partitions of a set subject to, respectively, union operations that merge two sets or refinement operations that split one set into two.

A disjoint union may mean one of two things. Most simply, it may mean the union of sets that are disjoint.[10] But if two or more sets are not already disjoint, their disjoint union may be formed by modifying the sets to make them disjoint before forming the union of the modified sets.[11] For instance two sets may be made disjoint by replacing each element by an ordered pair of the element and a binary value indicating whether it belongs to the first or second set.[12] For families of more than sets, one may similarly replace each element by an ordered pair of the element and the index of the set that contains it.[13]

See also

References

  1. ↑ 1.0 1.1 1.2 1.3 Halmos, P. R. (1960), Naive Set Theory, Undergraduate Texts in Mathematics, Springer, p. 15, ISBN 9780387900926 .
  2. ↑ Halbeisen, Lorenz J. (2011), Combinatorial Set Theory: With a Gentle Introduction to Forcing, Springer monographs in mathematics, Springer, p. 184, ISBN 9781447121732 .
  3. ↑ Copson, Edward Thomas (1988), Metric Spaces, Cambridge Tracts in Mathematics 57, Cambridge University Press, p. 62, ISBN 9780521357326 .
  4. ↑ Oberste-Vorth, Ralph W.; Mouzakitis, Aristides; Lawrence, Bonita A. (2012), Bridge to Abstract Mathematics, MAA textbooks, Mathematical Association of America, p. 59, ISBN 9780883857793 .
  5. ↑ Smith, Douglas; Eggen, Maurice; St. Andre, Richard (2010), A Transition to Advanced Mathematics, Cengage Learning, p. 95, ISBN 9780495562023 .
  6. ↑ Bollobás, Béla (1986), Combinatorics: Set Systems, Hypergraphs, Families of Vectors, and Combinatorial Probability, Cambridge University Press, p. 82, ISBN 9780521337038 .
  7. ↑ 7.0 7.1 Halmos (1960), p. 28.
  8. ↑ Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001), "Chapter 21: Data structures for Disjoint Sets", Introduction to Algorithms (Second ed.), MIT Press, pp. 498–524, ISBN 0-262-03293-7 .
  9. ↑ Paige, Robert; Tarjan, Robert E. (1987), "Three partition refinement algorithms", SIAM Journal on Computing 16 (6): 973–989, doi:10.1137/0216062, MR 917035 .
  10. ↑ Ferland, Kevin (2008), Discrete Mathematics: An Introduction to Proofs and Combinatorics, Cengage Learning, p. 45, ISBN 9780618415380 .
  11. ↑ Arbib, Michael A.; Kfoury, A. J.; Moll, Robert N. (1981), A Basis for Theoretical Computer Science, The AKM series in Theoretical Computer Science: Texts and monographs in computer science, Springer-Verlag, p. 9, ISBN 9783540905738 .
  12. ↑ Monin, Jean François; Hinchey, Michael Gerard (2003), Understanding Formal Methods, Springer, p. 21, ISBN 9781852332471 .
  13. ↑ Lee, John M. (2010), Introduction to Topological Manifolds, Graduate Texts in Mathematics 202 (2nd ed.), Springer, p. 64, ISBN 9781441979407 .

External links

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.