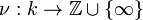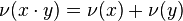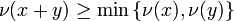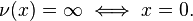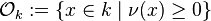Discrete valuation

From Wikipedia, the free encyclopedia

In mathematics, a discrete valuation is an integer valuation on a field k, that is a function

$\nu :k\to {\mathbb Z}\cup \{\infty \}$

satisfying the conditions

$\nu (x\cdot y)=\nu (x)+\nu (y)$

$\nu (x+y)\geq \min {\big \{}\nu (x),\nu (y){\big \}}$

$\nu (x)=\infty \iff x=0.$

Note that often the trivial valuation which takes on only the values $0,\infty$ is explicitly excluded.

A field with a non-trivial discrete valuation is called a discrete valuation field.

Discrete valuation rings and valuations on fields

To every field with discrete valuation $\nu$ we can associate the subring

${\mathcal {O}}_{k}:=\left\{x\in k\mid \nu (x)\geq 0\right\}$

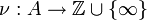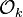of $k$ , which is a discrete valuation ring. Conversely, the valuation $\nu :A\rightarrow \mathbb{Z } \cup \{\infty \}$ on a discrete valuation ring $A$ can be extended to a valuation on the quotient field ${\text{Quot}}(A)$ giving a discrete valued field $k$ , whose associated discrete valuation ring ${\mathcal {O}}_{k}$ is just $A$ .

Examples

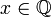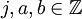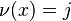For a fixed prime $p$ for any element $x\in {\mathbb {Q}}$ different from zero write $x=p^{j}{\frac {a}{b}}$ with $j,a,b\in \mathbb{Z }$ such that $p$ does not divide $a,b$ , then $\nu (x)=j$ is a valuation, called the p-adic valuation.

References

Fesenko, Ivan B.; Vostokov, Sergei V. (2002), Local fields and their extensions, Translations of Mathematical Monographs 121 (Second ed.), Providence, RI: American Mathematical Society, ISBN 978-0-8218-3259-2, MR 1915966

Discrete valuation

Discrete valuation rings and valuations on fields

Examples

References

See also