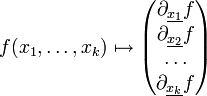
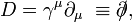Dirac operator

From Wikipedia, the free encyclopedia

In mathematics and quantum mechanics, a Dirac operator is a differential operator that is a formal square root, or half-iterate, of a second-order operator such as a Laplacian. The original case which concerned Paul Dirac was to factorise formally an operator for Minkowski space, to get a form of quantum theory compatible with special relativity; to get the relevant Laplacian as a product of first-order operators he introduced spinors.

In general, let D be a first-order differential operator acting on a vector bundle V over a Riemannian manifold M. If

D^{2}=\Delta ,\,

where ∆ is the Laplacian of V, then D is called a Dirac operator.

In high-energy physics, this requirement is often relaxed: only the second-order part of D2 must equal the Laplacian.

Examples

Example 1: D=-i ∂x is a Dirac operator on the tangent bundle over a line.

Example 2: We now consider a simple bundle of importance in physics: The configuration space of a particle with spin ½ confined to a plane, which is also the base manifold. It's represented by a wavefunction ψ: R2 → C2

\psi (x,y)={\begin{bmatrix}\chi (x,y)\\\eta (x,y)\end{bmatrix}}

where x and y are the usual coordinate functions on R2. χ specifies the probability amplitude for the particle to be in the spin-up state, and similarly for η. The so-called spin-Dirac operator can then be written

D=-i\sigma _{x}\partial _{x}-i\sigma _{y}\partial _{y},\,

where σi are the Pauli matrices. Note that the anticommutation relations for the Pauli matrices make the proof of the above defining property trivial. Those relations define the notion of a Clifford algebra.

Solutions to the Dirac equation for spinor fields are often called harmonic spinors.

Example 3: The most famous Dirac operator describes the propagation of a free fermion in three dimensions and is elegantly written

D=\gamma ^{\mu }\partial _{\mu }\ \equiv \partial \!\!\!/,

using the Feynman slash notation.

Example 4: There is also the Dirac operator arising in Clifford analysis. In euclidean n-space this is

D=\sum _{{j=1}}^{{n}}e_{{j}}{\frac {\partial }{\partial x_{{j}}}}

where {ej: j = 1, ..., n} is an orthonormal basis for euclidean n-space, and Rn is considered to be embedded in a Clifford algebra.

This is a special case of the Atiyah-Singer-Dirac operator acting on sections of a spinor bundle.

Example 5: For a spin manifold, M, the Atiyah-Singer-Dirac operator is locally defined as follows: For x ∈ M and e1(x), ..., ej(x) a local orthonormal basis for the tangent space of M at x, the Atiyah-Singer-Dirac operator is

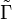\sum _{{j=1}}^{{n}}e_{{j}}(x){\tilde {\Gamma }}_{{e_{{j}}(x)}},

where {\tilde {\Gamma }} is a lifting of the Levi-Civita connection on M to the spinor bundle over M.

Generalisations

In Clifford analysis, the operator D: C∞(Rk ⊗ Rn, S) → C∞(Rk ⊗ Rn, Ck ⊗ S) acting on spinor valued functions defined by

f(x_{1},\ldots ,x_{k})\mapsto {\begin{pmatrix}\partial _{{\underline {x_{1}}}}f\\\partial _{{\underline {x_{2}}}}f\\\ldots \\\partial _{{\underline {x_{k}}}}f\\\end{pmatrix}}

is sometimes called Dirac operator in k Clifford variables. In the notation, S is the space of spinors, 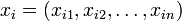x_{i}=(x_{{i1}},x_{{i2}},\ldots ,x_{{in}}) are n-dimensional variables and 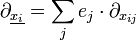\partial _{{\underline {x_{i}}}}=\sum _{j}e_{j}\cdot \partial _{{x_{{ij}}}} is the Dirac operator in the i-th variable. This is a common generalization of the Dirac operator (k=1) and the Dolbeault operator (n=2, k arbitrary). It is an invariant differential operator, invariant under the action of the group SL(k) × Spin(n). The resolution of D is known only in some special cases.

See also

References

    • Friedrich, Thomas (2000), Dirac Operators in Riemannian Geometry, American Mathematical Society, ISBN 978-0-8218-2055-1 
    • Colombo, F., I.; Sabadini, I. (2004), Analysis of Dirac Systems and Computational Algebra, Birkhauser Verlag AG, ISBN 978-3-7643-4255-5 
    This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.