Differentiated Bertrand competition
From Wikipedia, the free encyclopedia
As a solution to the Bertrand paradox in economics, it has been suggested that each firm produces a somewhat differentiated product, and consequently faces a demand curve that is downward-sloping for all levels of the firm's price.
An increase in a competitor's price is represented as an increase (for example, an upward shift) of the firm's demand curve.
As a result, when a competitor raises price, generally a firm can also raise its own price and increase its profits.
Calculating the differentiated Bertrand model
- q1 = firm 1’s demand, *q1≥0
- q2 = firm 2’s demand, *q1≥0
- A1 = Constant in equation for firm 1’s demand
- A2 = Constant in equation for firm 2’s demand
- a1 = slope coefficient for firm 1’s price
- a2 = slope coefficient for firm 2’s price
- p1 = firm 1’s price level pr unit
- p2 = firm 2’s price level pr unit
- b1 = slope coefficient for how much firm 2's price affects firm 1's demand
- b2 = slope coefficient for how much firm 1's price affects firm 2's demand
- q1=A1-a1*p1+b1*p2
- q2=A2-a2*p2+b2*p1
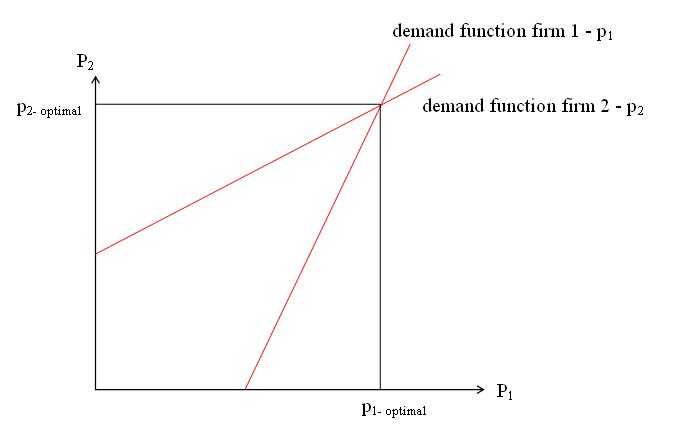
The above figure presents the best response functions of the firms, which are complements to each other.
Uses
Merger simulation models ordinarily assume differentiated Bertrand competition within a market that includes the merging firms.
See also
- Bertrand competition
- Bertrand paradox (economics)
- Oligopoly theory
External sources
- Oligoply Theory made Simple, Chapter 6 of Surfing Economics by Huw Dixon.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.