Diamond principle

From Wikipedia, the free encyclopedia

In mathematics, and particularly in axiomatic set theory, the diamond principle ◊ is a combinatorial principle introduced by Ronald Jensen in Jensen (1972) that holds in the constructible universe and that implies the continuum hypothesis. Jensen extracted the diamond principle from his proof that V=L implies the existence of a Suslin tree.

Definition

The diamond principle ◊ says that there exists a ◊-sequence, in other words sets Aα⊆α for α<ω1 such that for any subset A of ω1 the set of α with A∩α = Aα is stationary in ω1.

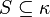More generally, for a given cardinal number \kappa and a stationary set S\subseteq \kappa , the statement ◊S (sometimes written ◊(S) or ◊κ(S)) is the statement that there is a sequence 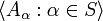\langle A_{\alpha }:\alpha \in S\rangle such that

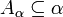
  • each A_{\alpha }\subseteq \alpha
  • for every 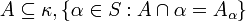A\subseteq \kappa ,\{\alpha \in S:A\cap \alpha =A_{\alpha }\} is stationary in \kappa

The principle ◊ω1 is the same as ◊.

Properties and use

Jensen (1972) showed that the diamond principle ◊ implies the existence of Suslin trees. He also showed that ◊ implies the CH. Also ♣ + CH implies ◊, but Shelah gave models of ♣ + ¬ CH, so ◊ and ♣ are not equivalent (rather, ♣ is weaker than ◊).

Akemann & Weaver (2004) used ◊ to construct a C*-algebra serving as a counterexample to Naimark's problem.

For all cardinals κ and stationary subsets S⊆κ+, ◊S holds in the constructible universe. Recently Shelah proved that for κ>ℵ0, ◊κ+ follows from 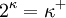2^{\kappa }=\kappa ^{+}.

See also

References

  • Akemann, Charles; Weaver, Nik (2004), "Consistency of a counterexample to Naimark's problem", Proceedings of the National Academy of Sciences of the United States of America 101 (20): 7522–7525, arXiv:math.OA/0312135, doi:10.1073/pnas.0401489101, MR 2057719 
  • Jensen, R. Björn (1972), "The fine structure of the constructible hierarchy", Annals of Mathematical lLogic 4: 229–308, doi:10.1016/0003-4843(72)90001-0, MR 0309729 
  • Assaf Rinot, Jensen's diamond principle and its relatives, online
  • S. Shelah: Whitehead groups may not be free, even assuming CH, II, Israel J. Math., 35(1980), 257–285.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.