Dense subgraph
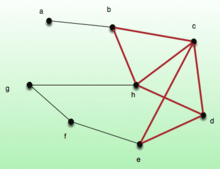
 with density
with density  and it's densest subgraph induced by the vertices
and it's densest subgraph induced by the vertices  and
and  in red with density
in red with density 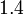
In computer science the notion of highly connected subgraphs appears frequently. This notion can be formalized as follows. Let 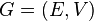 be an undirected graph and let
be an undirected graph and let 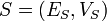 be a subgraph of
be a subgraph of  . Then the density of
. Then the density of 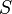 is defined to be
is defined to be 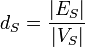 .
.
The densest subgraph problem is that of finding a subgraph of maximum density. In 1984, Andrew V. Goldberg developed a polynomial time algorithm to find the maximum density subgraph using a max flow technique.
Densest  subgraph
subgraph
There are many variations on the densest subgraph problem. There is the densest  subgraph problem, where the objective is to find the maximum density subgraph on exactly
subgraph problem, where the objective is to find the maximum density subgraph on exactly  vertices. This problem is known to be NP-Hard by a reduction from the clique problem. The densest
vertices. This problem is known to be NP-Hard by a reduction from the clique problem. The densest  subgraph problem is NP-Complete even in planar graphs by a reduction from the connected vertex cover problem on planar graphs with maximum degree 4. There does not exist a polynomial-time approximation scheme (PTAS) for the densest
subgraph problem is NP-Complete even in planar graphs by a reduction from the connected vertex cover problem on planar graphs with maximum degree 4. There does not exist a polynomial-time approximation scheme (PTAS) for the densest  subgraph problem this is by a reduction from the Minimum Distance of Code problem.
subgraph problem this is by a reduction from the Minimum Distance of Code problem.
Densest at most  subgraph
subgraph
The objective of the densest at most  problem is to find the maximum density subgraph on at most
problem is to find the maximum density subgraph on at most  vertices. Anderson and Chellapilla showed that if there exists an
vertices. Anderson and Chellapilla showed that if there exists an  approximation for this problem then that will lead to an
approximation for this problem then that will lead to an 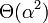 approximation for the densest
approximation for the densest  subgraph problem.
subgraph problem.
Densest at least  subgraph
subgraph
The densest at least  problem is defined similarly to the densest at most
problem is defined similarly to the densest at most  subgraph problem. There is a 2-approximation due to Anderson. But the complexity of this problem is still unknown.
subgraph problem. There is a 2-approximation due to Anderson. But the complexity of this problem is still unknown.
References
- Goldberg, A. V. (1984), "Finding a maximum density subgraph", Technical report.
- Feige, U.; Kortsarz, G.; Peleg, D. (1997), "The dense k-subgraph problem", Algorithmica 29: 410–421.
- Keil, J.; Brecht, T. (1991), "The complexity of clustering in planar graphs", The Journal of Combinatorial Mathematics and Combinatorial Computing 9: 155–159.
- Khot, S. (2006), "Ruling out PTAS for graph min-bisection, dense k-subgraph, and bipartite clique", SIAM Journal on Computing 36: 1025–1071.
- Anderson, R.; Chellapilla, K. (2009), "Finding dense subgraphs with size bounds", WAW: 25–36.
- Anderson, R. (2007), "Finding large and small dense subgraphs", CoRR.
- Khuller, S.; Saha, B. (2009), "On finding dense subgraphs", The International Colloquium on Automata, Languages and Programming.