Dense-in-itself

From Wikipedia, the free encyclopedia

In mathematics, a subset $A$ of a topological space is said to be dense-in-itself if $A$ contains no isolated points.

Every dense-in-itself closed set is perfect. Conversely, every perfect set is dense-in-itself.

A simple example of a set which is dense-in-itself but not closed (and hence not a perfect set) is the subset of irrational numbers (considered as a subset of the real numbers). This set is dense-in-itself because every neighborhood of an irrational number $x$ contains at least one other irrational number $y\neq x$ . On the other hand, this set of irrationals is not closed because every rational number lies in its closure. For similar reasons, the set of rational numbers (also considered as a subset of the real numbers) is also dense-in-itself but not closed.

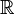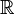The above examples, the irrationals and the rationals, are also dense sets in their topological space, namely ${\mathbb {R}}$ . As an example that is dense-in-itself but not dense in its topological space, consider ${\mathbb {Q}}\cap [0,1]$ . This set is not dense in ${\mathbb {R}}$ but is dense-in-itself.

It is also interesting to note, although tautological, that the domain of a continuous function must be the union of dense-in-itself sets and/or isolated points.^{[citation needed]}

References

Steen, Lynn Arthur; Seebach, J. Arthur Jr.. Counterexamples in Topology (Dover reprint of 1978 ed.). Berlin, New York: Springer-Verlag. p. 6. ISBN 978-0-486-68735-3. MR 507446.

This article incorporates material from Dense in-itself on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Dense-in-itself

See also

References