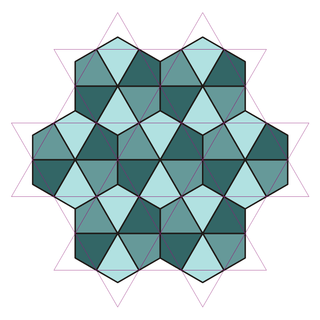
Deltoidal trihexagonal tiling
| Deltoidal trihexagonal tiling | |
|---|---|
 | |
| Type | Dual semiregular tiling |
| Coxeter-Dynkin diagram | |
| Faces | kite |
| Face configuration | V3.4.6.4 |
| Symmetry group | p6m, [6,3], (*632) |
| Rotation group | p6, [6,3]+, (632) |
| Dual | Rhombitrihexagonal tiling |
| Properties | face-transitive |
In geometry, the deltoidal trihexagonal tiling is a dual of the semiregular tiling known as the rhombitrihexagonal tiling. Conway calls it a tetrille.[1] The edges of this tiling can be formed by the intersection overlay of the regular triangular tiling and a hexagonal tiling. Each kite face of this tiling has angles 120°, 90°, 60° and 90°. It is one of only eight tilings of the plane in which every edge lies on a line of symmetry of the tiling.[2]
Dual tiling
The deltoidal trihexagonal tiling is a dual of the semiregular tiling rhombitrihexagonal tiling.[3] Its faces are deltoids or kites.
Related polyhedra and tilings
This tiling has face transitive variations, that can distort the kites into bilateral trapezoids or more general quadrillaterals. Ignoring the face colors below, the fully symmetry is p6m, and the lower symmetry is p31m with 3 mirrors meeting at a point, and 3-fold rotation points.[4]
| Symmetry | p6m, [6,3], (*632) | p31m, [6,3+], (3*3) | |
|---|---|---|---|
| Form |  |
 |
 |
| Faces | Kite | Half regular hexagon | Quadrilaterals |
This tiling is related to the trihexagonal tiling by dividing the triangles and hexagons into central triangles and merging neighboring triangles into kites.
This tiling is topologically related as a part of sequence of cantellated polyhedra with vertex figure (3.4.n.4), and continues as tilings of the hyperbolic plane. These vertex-transitive figures have (*n32) reflectional symmetry.
| Symmetry *n32 [n,3] |
Spherical | Euclidean | Hyperbolic... | |||||
|---|---|---|---|---|---|---|---|---|
| *232 [2,3] D3h |
*332 [3,3] Td |
*432 [4,3] Oh |
*532 [5,3] Ih |
*632 [6,3] P6m |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] | |
| Expanded figure |
3.4.2.4 |
 3.4.3.4 |
 3.4.4.4 |
 3.4.5.4 |
 3.4.6.4 |
3.4.7.4 |
3.4.8.4 |
 3.4.∞.4 |
| Coxeter Schläfli |
rr{2,3} |
rr{3,3} |
rr{4,3} |
rr{5,3} |
rr{6,3} |
rr{7,3} |
rr{8,3} |
rr{∞,3} |
| Deltoidal figure |  V3.4.2.4 |
V3.4.3.4 |
 V3.4.4.4 |
V3.4.5.4 |
 V3.4.6.4 |
 V3.4.7.4 |
 V3.4.8.4 |
 V3.4.∞.4 |
| Coxeter | ||||||||
The deltoidal trihexagonal tiling is a part of a set of uniform dual tilings, corresponding to the dual of the rhombitrihexagonal tiling.
| Symmetry: [6,3], (*632) | [6,3]+ (632) |
[1+,6,3] (*333) |
[6,3+] (3*3) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| {6,3} | t{6,3} | r{6,3} r{3[3]} |
t{3,6} t{3[3]} |
{3,6} {3[3]} |
rr{6,3} s2{6,3} |
tr{6,3} | sr{6,3} | h{6,3} {3[3]} |
h2{6,3} r{3[3]} |
s{3,6} s{3[3]} |
= |
= |
= |
= | |||||||
| Uniform duals | ||||||||||
| V63 | V3.122 | V(3.6)2 | V63 | V36 | V3.4.12.4 | V.4.6.12 | V34.6 | V36 | V(3.6)2 | V36 |
Other deltoidal (kite) tiling
Other deltoidal tilings are possible.
Point symmetry allows the plane to be filled by growing kites, with the topology as a square tiling, V4.4.4.4, and can be created by crossing string of a dream catcher. Below is an example with dihedral hexagonal symmetry.
Another face transitive tiling with kite faces, also a topological variation of a square tiling and with face configuration V4.4.4.4. It is also vertex transitive, with every vertex containing all orientations of the kite face.
| Symmetry | D6, [6], (*66) | pmg, [∞,(2,∞)+], (22*) | p6m, [6,3], (*632) |
|---|---|---|---|
| Tiling |  |
 |
 |
| Configuration | V4.4.4.4 | V6.4.3.4 | |
See also
| Wikimedia Commons has media related to Deltoidal trihexagonal tiling. |
- Tilings of regular polygons
- List of uniform planar tilings
Notes
- ↑ Conway, 2008, p288 table
- ↑ Kirby, Matthew; Umble, Ronald (2011), "Edge tessellations and stamp folding puzzles", Mathematics Magazine 84 (4): 283–289, arXiv:0908.3257, doi:10.4169/math.mag.84.4.283, MR 2843659.
- ↑ Weisstein, Eric W., "Dual tessellation", MathWorld. (See comparative overlay of this tiling and its dual)
- ↑ Tilings and Patterns
References
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. p40
- Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman and Company. ISBN 0-7167-1193-1. (Page 476, Tilings by polygons, #41 of 56 polygonal isohedral types by quadrangles)
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 21, Naming Archimedean and Catalan polyhedra and tilings)