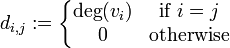Degree matrix

From Wikipedia, the free encyclopedia

In the mathematical field of graph theory the degree matrix is a diagonal matrix which contains information about the degree of each vertex—that is, the number of edges attached to each vertex. It is used together with the adjacency matrix to construct the Laplacian matrix of a graph.

Definition

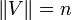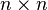Given a graph $G=(V,E)$ with $\|V\|=n$ the degree matrix $D$ for $G$ is a $n\times n$ diagonal matrix defined as

$d_{{i,j}}:=\left\{{\begin{matrix}\deg(v_{i})&{\mbox{if}}\ i=j\\0&{\mbox{otherwise}}\end{matrix}}\right.$

where the degree $\deg(v_{i})$ of a vertex counts the number of times an edge terminates at that vertex. In an undirected graph, this means that each new loop increases the degree of a vertex by two. In a directed graph, the term degree may refer either to indegree (the number of incoming edges at each vertex) or outdegree (the number of outgoing edges at each vertex).

Example

Vertex labeled graph	Degree matrix
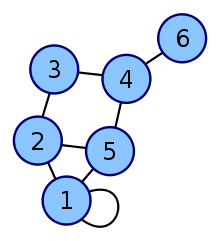	${\begin{pmatrix}4&0&0&0&0&0\\0&3&0&0&0&0\\0&0&2&0&0&0\\0&0&0&3&0&0\\0&0&0&0&3&0\\0&0&0&0&0&1\\\end{pmatrix}}$

The degree matrix of a k-regular graph has a constant diagonal of $k$

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.