David Harbater

From Wikipedia, the free encyclopedia

David Harbater

Born	(1952-12-19) December 19, 1952 New York City, New York, USA
Nationality	American
Fields	Mathematics
Institutions	University of Pennsylvania
Alma mater	MIT Brandeis University Harvard University
Doctoral advisor	Michael Artin
Doctoral students	Sybilla Beckmann Eric Dew Ryan Eberhart Shuvra Gupta Hilaf Hasson Tamara Lefcourt Claus-Georg Lehr Jing Long Hoelscher Andrew Obus Rachel Pries Katherine Stevenson Cui Yin
Known for	Proof of Abhyankar's conjecture
Notable awards	Cole Prize (1995)

David Harbater (born December 19, 1952) is an American mathematician at the University of Pennsylvania, well known for his work in Galois theory, algebraic geometry and arithmetic geometry.

Life and work

Harbater was born in New York City and attended Stuyvesant High School, where he was on the math team. After graduating in 1970, he entered Harvard University.

After graduating summa cum laude in 1974, Harbater earned a master's degree from Brandeis University and then a Ph.D. in 1978 from MIT, where he wrote a dissertation (Deformation Theory and the Fundamental Group in Algebraic Geometry) under the direction of Michael Artin.

In 1995, Harbater was awarded the Cole Prize for his solution, with Michel Raynaud, of the long outstanding Abhyankar conjecture. He has also solved the inverse Galois problem over 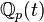${\mathbb {Q}}_{p}(t)$ , and made many other significant contributions to the field of Galois theory.

In 2012 he became a fellow of the American Mathematical Society.^[1]

Harbater's recent work on patching over fields, together with Julia Hartmann and Daniel Krashen, has had applications in such varied fields as quadratic forms, central simple algebras and local-global principles.

References

↑ List of Fellows of the American Mathematical Society, retrieved 2013-01-19.

Harbater, D. (1994). "Abhyankar's Conjecture on Galois Groups Over Curves". Invent. Math. 117 (1): 1–25. doi:10.1007/BF01232232.

External links

Persondata
Name	Harbater, David
Alternative names
Short description	American mathematician
Date of birth	December 19, 1952
Place of birth	New York City, New York, USA
Date of death
Place of death

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.