Daniel Goldston
| Daniel Goldston | |
|---|---|
 | |
| Born |
January 4, 1954 Oakland, California |
| Nationality | American |
| Fields | Mathematics |
| Institutions | San Jose State University |
| Alma mater | UC Berkeley |
Daniel Alan Goldston (born January 4, 1954 in Oakland, California) is an American mathematician who specializes in number theory. He is currently a professor of mathematics at San Jose State University.
Goldston is best known for the following result that he, János Pintz, and Cem Yıldırım proved in 2005:[1]
where 
denotes the nth prime number. In other words, for every 
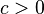, there exist infinitely many pairs of consecutive primes and 
which are closer to each other than the average distance between consecutive primes by a factor of 
, i.e., 
.
This result was originally reported in 2003 by Dan Goldston and Cem Yıldırım but was later retracted.[2][3] Then Janos Pintz joined the team and they completed the proof in 2005.
In fact, if they assume the Elliott–Halberstam conjecture, then they can also show that primes within 16 of each other occur infinitely often, which is related to the twin prime conjecture.