Cylindric algebra

From Wikipedia, the free encyclopedia

The notion of cylindric algebra, invented by Alfred Tarski, arises naturally in the algebraization of first-order logic with equality. This is comparable to the role Boolean algebras play for propositional logic. Indeed, cylindric algebras are Boolean algebras equipped with additional cylindrification operations that model quantification and equality. They differ from polyadic algebras in that the latter do not model equality.

Definition of a cylindric algebra

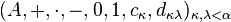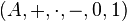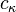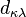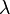A cylindric algebra of dimension $\alpha$ (where $\alpha$ is any ordinal number) is an algebraic structure $(A,+,\cdot ,-,0,1,c_{\kappa },d_{{\kappa \lambda }})_{{\kappa ,\lambda <\alpha }}$ such that $(A,+,\cdot ,-,0,1)$ is a Boolean algebra, $c_{\kappa }$ a unary operator on $A$ for every $\kappa$ , and $d_{{\kappa \lambda }}$ a distinguished element of $A$ for every $\kappa$ and $\lambda$ , such that the following hold:

(C1) 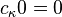$c_{\kappa }0=0$

(C2) 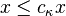$x\leq c_{\kappa }x$

(C3) $c_{\kappa }(x\cdot c_{\kappa }y)=c_{\kappa }x\cdot c_{\kappa }y$

(C4) $c_{\kappa }c_{\lambda }x=c_{\lambda }c_{\kappa }x$

(C5) $d_{{\kappa \kappa }}=1$

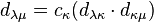
(C6) If $\kappa \neq \lambda \mu$ , then $d_{{\lambda \mu }}=c_{\kappa }(d_{{\lambda \kappa }}\cdot d_{{\kappa \mu }})$

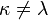(C7) If $\kappa \neq \lambda$ , then $c_{\kappa }(d_{{\kappa \lambda }}\cdot x)\cdot c_{\kappa }(d_{{\kappa \lambda }}\cdot -x)=0$

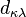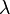Assuming a presentation of first-order logic without function symbols, the operator $c_{\kappa }x$ models existential quantification over variable $\kappa$ in formula $x$ while the operator $d_{{\kappa \lambda }}$ models the equality of variables $\kappa$ and $\lambda$ . Henceforth, reformulated using standard logical notations, the axioms read as

(C1) 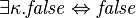$\exists \kappa .{\mathit {false}}\Leftrightarrow {\mathit {false}}$

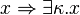
(C2) $x\Rightarrow \exists \kappa .x$

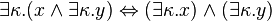
(C3) $\exists \kappa .(x\wedge \exists \kappa .y)\Leftrightarrow (\exists \kappa .x)\wedge (\exists \kappa .y)$

(C4) $\exists \kappa \exists \lambda .x\Leftrightarrow \exists \lambda \exists \kappa .x$

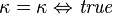
(C5) $\kappa =\kappa \Leftrightarrow {\mathit {true}}$

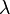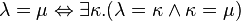
(C6) If $\kappa$ is a variable different from both $\lambda$ and $\mu$ , then $\lambda =\mu \Leftrightarrow \exists \kappa .(\lambda =\kappa \wedge \kappa =\mu )$

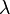(C7) If $\kappa$ and $\lambda$ are different variables, then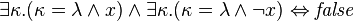 $\exists \kappa .(\kappa =\lambda \wedge x)\wedge \exists \kappa .(\kappa =\lambda \wedge \neg x)\Leftrightarrow {\mathit {false}}$

Generalizations

Recently, cylindric algebras have been generalized to the many-sorted case, which allows for a better modeling of the duality between first-order formulas and terms.

References

Leon Henkin, Monk, J.D., and Alfred Tarski (1971) Cylindric Algebras, Part I. North-Holland. ISBN 978-0-7204-2043-2.
-------- (1985) Cylindric Algebras, Part II. North-Holland.
Carlos Caleiro, Ricardo Gonçalves (2006). "On the algebraization of many-sorted logics". In J. Fiadeiro and P.-Y. Schobbens. Proc. 18th int. conf. on Recent trends in algebraic development techniques (WADT). LNCS 4409. Springer. pp. 21–36. ISBN 978-3-540-71997-7.

Cylindric algebra

Definition of a cylindric algebra

Generalizations

See also

References

Further reading