Cyclic code
In coding theory, cyclic codes are linear block error-correcting codes that have convenient algebraic structures for efficient error detection and correction.
Definition
Let 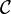 be a linear code over a finite field
be a linear code over a finite field  of block length n.
of block length n. 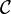 is called a cyclic code if, for every codeword c=(c1,...,cn) from C, the word (cn,c1,...,cn-1) in
is called a cyclic code if, for every codeword c=(c1,...,cn) from C, the word (cn,c1,...,cn-1) in  obtained by a cyclic right shift of components is again a codeword. Because one cyclic right shift is equal to n − 1 cyclic left shifts, a cyclic code may also be defined via cyclic left shifts. Therefore the linear code
obtained by a cyclic right shift of components is again a codeword. Because one cyclic right shift is equal to n − 1 cyclic left shifts, a cyclic code may also be defined via cyclic left shifts. Therefore the linear code 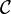 is cyclic precisely when it is invariant under all cyclic shifts.
is cyclic precisely when it is invariant under all cyclic shifts.
Cyclic Codes have some additional structural constraint on the codes. They are based on Galois fields and because of their structural properties they are very useful for error controls. Their structure is strongly related to Galois fields because of which the encoding and decoding algorithms for cyclic codes are computationally efficient.
Algebraic structure
Cyclic codes can be linked to ideals in certain rings. Let ![R=A[x]/(x^{n}-1)](/2014-wikipedia_en_all_02_2014/I/media/1/a/e/2/1ae2ccbe035e336b8df952339363a56a.png) be a polynomial ring over the finite field
be a polynomial ring over the finite field 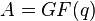 . Identify the elements of the cyclic code C with polynomials in R such that
. Identify the elements of the cyclic code C with polynomials in R such that
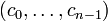 maps to the polynomial
maps to the polynomial
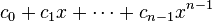 : thus multiplication by x corresponds to a cyclic shift. Then C is an ideal in R, and hence principal, since R is a principal ideal ring. The ideal is generated by the unique monic element in C of minimum degree, the generator polynomial g.[1]
This must be a divisor of
: thus multiplication by x corresponds to a cyclic shift. Then C is an ideal in R, and hence principal, since R is a principal ideal ring. The ideal is generated by the unique monic element in C of minimum degree, the generator polynomial g.[1]
This must be a divisor of  . It follows that every cyclic code is a polynomial code.
If the generator polynomial g has degree d then the rank of the code C is
. It follows that every cyclic code is a polynomial code.
If the generator polynomial g has degree d then the rank of the code C is 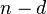 .
.
The idempotent of C is a codeword e such that e2 = e (that is, e is an idempotent element of C) and e is an identity for the code, that is e c = c for every codeword c. If n and q are coprime such a word always exists and is unique;[2] it is a generator of the code.
An irreducible code is a cyclic code in which the code, as an ideal, is maximal in R, so that its generator is an irreducible polynomial.
Examples
For example, if A= and n=3, the set of codewords contained in the (1,1,0)-cyclic code is precisely
and n=3, the set of codewords contained in the (1,1,0)-cyclic code is precisely
 .
.
It corresponds to the ideal in ![{\mathbb {F}}_{2}[x]/(x^{3}-1)](/2014-wikipedia_en_all_02_2014/I/media/5/0/3/f/503fb4dad4997ec75a269dbdd645db08.png) generated by
generated by 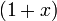 .
.
Note that 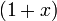 is an irreducible polynomial in the polynomial ring, and hence the code is an irreducible code.
is an irreducible polynomial in the polynomial ring, and hence the code is an irreducible code.
The idempotent of this code is the polynomial  , corresponding to the codeword (1,1,0).
, corresponding to the codeword (1,1,0).
Trivial examples
Trivial examples of cyclic codes are An itself and the code containing only the zero codeword. These correspond to generators 1 and  respectively: these two polynomials must always be factors of
respectively: these two polynomials must always be factors of  .
.
Over GF(2) the parity bit code, consisting of all words of even weight, corresponds to generator  . Again over GF(2) this must always be a factor of
. Again over GF(2) this must always be a factor of  .
.
Quasi-cyclic codes and shortened codes
Before delving into the details of cyclic codes first we will discuss quasi-cyclic and shortened codes which are closely related to the cyclic codes and they all can be converted into each other.
Definition
Quasi-cyclic codes:
An 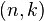 quasi-cyclic code is a linear block code such that, for some
quasi-cyclic code is a linear block code such that, for some  coprime with
coprime with  , the polynomial
, the polynomial 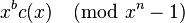 is a codeword polynomial whenever
is a codeword polynomial whenever 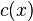 is a codeword polynomial.
is a codeword polynomial.
Here codeword polynomial is a linear code whose code words are polynomials that are divisible by a polynomial of shorter length called generator polynomial. Note that every codeword polynomial can be expressed in the form 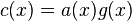 . For any codeword
. For any codeword 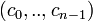 codeword polynomial corresponds to the
codeword polynomial corresponds to the 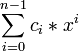 .
.
Definition
Shortened codes:
An ![[n,k]](/2014-wikipedia_en_all_02_2014/I/media/3/a/5/3/3a53f37178a6264d7a2224c47bafea26.png) linear code is called a proper shortened cyclic code if it can be obtained by deleting
linear code is called a proper shortened cyclic code if it can be obtained by deleting  positions from an
positions from an 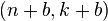 cyclic code.
cyclic code.
In shortened codes information symbols are deleted to obtain a desired blocklength smaller than the design blocklength. The missing information symbols are usually imagined to be at the beginning of the codeword and are considered to be 0. Therefore,  −
− is fixed, and then
is fixed, and then  is decreased which eventually decreases
is decreased which eventually decreases  . Note that it is not necessary to delete the starting symbols. Depending on the application sometimes consecutive positions are considered as 0 and are deleted.
. Note that it is not necessary to delete the starting symbols. Depending on the application sometimes consecutive positions are considered as 0 and are deleted.
All the symbols which are dropped need not be transmitted and at the receiving end can be reinserted. To convert 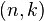 cyclic code to
cyclic code to  shortened code, set
shortened code, set  symbols to zero and drop them from each codeword. Any cyclic code can be converted to quasi-cyclic codes by dropping every
symbols to zero and drop them from each codeword. Any cyclic code can be converted to quasi-cyclic codes by dropping every  th symbol where
th symbol where  is a factor of
is a factor of  . If the dropped symbols are not check symbols then this cyclic code is also a shortened code.
. If the dropped symbols are not check symbols then this cyclic code is also a shortened code.
Cyclic codes for correcting errors
Now, we will begin the discussion of cyclic codes explicitly with error detection and correction. Cyclic codes can be used to correct errors, like Hamming codes as a cyclic codes can be used for correcting single error. Likewise, they are also used to correct double errors and burst errors. All types of error corrections are covered briefly in the further subsections.
The (7,4) Hamming code has a generator polynomial  . This polynomial has a zero in Galois extension field
. This polynomial has a zero in Galois extension field 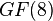 at the primitive element
at the primitive element  , and all codewords satisfy
, and all codewords satisfy 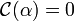 . Cyclic codes can also be used to correct double errors over the field
. Cyclic codes can also be used to correct double errors over the field  . Blocklength will be
. Blocklength will be  equal to
equal to 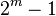 and primitive elements
and primitive elements  and
and  as zeros in the
as zeros in the 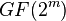 because we are considering the case of two errors here, so each will represent one error.
because we are considering the case of two errors here, so each will represent one error.
The received word is a polynomial of degree 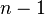 given as
given as
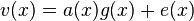
where  can have at most two nonzero coefficients corresponding to 2 errors.
can have at most two nonzero coefficients corresponding to 2 errors.
We define the Syndrome Polynomial,  as the remainder of polynomial
as the remainder of polynomial  when divided by the generator polynomial
when divided by the generator polynomial 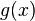 i.e.
i.e.
 =
=  as
as 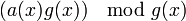 is zero.
is zero.
For correcting two errors
Let the field elements 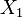 and
and  be the two error location numbers. If only one error occurs then
be the two error location numbers. If only one error occurs then  is equal to zero and if none occurs both are zero.
is equal to zero and if none occurs both are zero.
Let  and
and  .
.
These field elements are called "syndromes". Now because 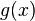 is zero at primitive elements
is zero at primitive elements  and
and  , so we can write
, so we can write 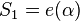 and
and 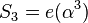 . If say two errors occur, then
. If say two errors occur, then
 and
and
 .
.
And these two can be considered as two pair of equations in 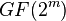 with two unknowns and hence we can write
with two unknowns and hence we can write
 and
and
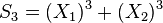 .
.
Hence if the two pair of nonlinear equations can be solved cyclic codes can used to correct two errors.
Hamming code
The Hamming(7,4) code may be written as a cyclic code over GF(2) with generator 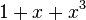 . In fact, any binary Hamming code of the form Ham(2,q) is equivalent to a cyclic code when
. In fact, any binary Hamming code of the form Ham(2,q) is equivalent to a cyclic code when  is even.[3] Hamming codes of the form Ham(r,2) are also cyclic when
is even.[3] Hamming codes of the form Ham(r,2) are also cyclic when 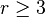 - they are
- they are ![[2^{{r}}-1,2^{{r}}-r-2,4]](/2014-wikipedia_en_all_02_2014/I/media/1/d/f/8/1df8a14937a2a8541b3b4c09ece2e29a.png) -codes.[4]
-codes.[4]
Hamming code for correcting single errors
A code whose minimum distance is at least 3, have a check matrix all of whose columns are distinct and non zero. If a check matrix for a binary code has  rows, then each column is an
rows, then each column is an  -bit binary number. There are
-bit binary number. There are 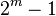 possible columns. Therefore if a check matrix of a binary code with
possible columns. Therefore if a check matrix of a binary code with  at least 3 has
at least 3 has  rows, then it can only have
rows, then it can only have 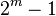 columns, not more than that. This defines a
columns, not more than that. This defines a  code, called Hamming code.
code, called Hamming code.
It is easy to define Hamming codes for large alphabets of size  . We need to define one
. We need to define one 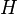 matrix with linearly independent columns. For any word of size
matrix with linearly independent columns. For any word of size  there will be columns who are multiples of each other. So, to get linear independence all non zero
there will be columns who are multiples of each other. So, to get linear independence all non zero  -tuples with one as a top most non zero element will be chosen as columns. Then two columns will never be linearly dependent because three columns could be linearly dependent with the minimum distance of the code as 3.
-tuples with one as a top most non zero element will be chosen as columns. Then two columns will never be linearly dependent because three columns could be linearly dependent with the minimum distance of the code as 3.
So, there are 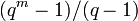 nonzero columns with one as top most non zero element. Therefore, Hamming code is a
nonzero columns with one as top most non zero element. Therefore, Hamming code is a ![[(q^{m}-1)/(q-1),(q^{m}-1)/(q-1)-m]](/2014-wikipedia_en_all_02_2014/I/media/7/6/3/4/7634c54de420544ed2029392befa526a.png) code.
code.
Now, for cyclic codes, Let  be primitive element in
be primitive element in 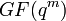 , and let
, and let  . Then
. Then  and thus
and thus  is a zero of the polynomial
is a zero of the polynomial 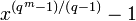 and is a generator polynomial for the cyclic code of block length
and is a generator polynomial for the cyclic code of block length 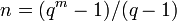 .
.
But for  ,
,  . And the received word is a polynomial of degree
. And the received word is a polynomial of degree 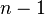 given as
given as
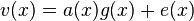
where, 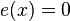 or
or 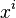 where
where  represents the error locations.
represents the error locations.
But we can also use 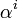 as an element of
as an element of 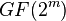 to index error location. Because
to index error location. Because 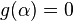 , we have
, we have 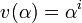 and all powers of
and all powers of  from
from  to
to 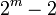 are distinct. Therefore we can easily determine error location
are distinct. Therefore we can easily determine error location  from
from 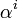 unless
unless 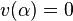 which represents no error. So, hamming code is a single error correcting code over
which represents no error. So, hamming code is a single error correcting code over  with
with 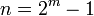 and
and 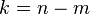 .
.
Cyclic codes for correcting burst errors
From Hamming distance concept, a code with minimum distance 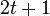 can correct any
can correct any  errors. But in many channels error pattern is not very arbitrary, it occurs within very short segment of the message. Such kind of errors are called burst errors. So, for correcting such errors we will get a more efficient code of higher rate because of the less constraints. Cyclic codes are used for correcting burst error. In fact, cyclic codes can also correct cyclic burst errors along with burst errors. Cyclic burst errors are defined as
errors. But in many channels error pattern is not very arbitrary, it occurs within very short segment of the message. Such kind of errors are called burst errors. So, for correcting such errors we will get a more efficient code of higher rate because of the less constraints. Cyclic codes are used for correcting burst error. In fact, cyclic codes can also correct cyclic burst errors along with burst errors. Cyclic burst errors are defined as
A cyclic burst of length  is a vector whose nonzero components are among
is a vector whose nonzero components are among  (cyclically) consecutive components, the first and the last of which are nonzero.
(cyclically) consecutive components, the first and the last of which are nonzero.
In polynomial form cyclic burst of length  can be described as
can be described as  with
with  as a polynomial of degree
as a polynomial of degree 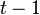 with nonzero coefficient
with nonzero coefficient 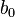 . Here
. Here  defines the pattern and
defines the pattern and 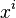 defines the starting point of error. Length of the pattern is given by deg
defines the starting point of error. Length of the pattern is given by deg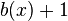 . Syndrome poynomial is unique for each pattern and is given by
. Syndrome poynomial is unique for each pattern and is given by
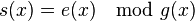
A linear block code that corrects all burst errors of length  or less must have at least
or less must have at least 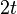 check symbols. Proof: Because any linear code that can correct burst pattern of length
check symbols. Proof: Because any linear code that can correct burst pattern of length  or less cannot have a burst of length
or less cannot have a burst of length 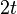 or less as a codeword because if it did then a burst of length
or less as a codeword because if it did then a burst of length  could change the codeword to burst pattern of length
could change the codeword to burst pattern of length  , which also could be obtained by making a burst error of length
, which also could be obtained by making a burst error of length  in all zero codeword. Now, any two vectors that are non zero in the first
in all zero codeword. Now, any two vectors that are non zero in the first 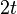 components must be from different co-sets of an array to avoid their difference being a codeword of bursts of length
components must be from different co-sets of an array to avoid their difference being a codeword of bursts of length 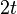 . Therefore number of such co-sets are equal to number of such vectors which are
. Therefore number of such co-sets are equal to number of such vectors which are 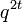 . Hence at least
. Hence at least 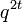 co-sets and hence at least
co-sets and hence at least 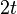 check symbol.
check symbol.
This property is also known as Rieger bound and it is similar to the singleton bound for random error correcting.
Fire codes as cyclic bounds
Fire code is a cyclic burst error correcting code over  with the generator polynomial
with the generator polynomial
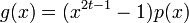
where  is a prime polynomial with degree
is a prime polynomial with degree  not smaller than
not smaller than  and
and  does not divide
does not divide  . Block length of the fire code is the smallest integer
. Block length of the fire code is the smallest integer  such that
such that 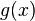 divides
divides
 .
.
A fire code can correct all burst errors of length t or less if no two bursts  and
and 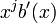 appear in the same co-set. This can be proved by contradiction. Suppose there are two distinct nonzero bursts
appear in the same co-set. This can be proved by contradiction. Suppose there are two distinct nonzero bursts  and
and 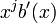 of length
of length  or less and are in the same co-set of the code. So, their difference is a codeword. As the difference is a multiple of
or less and are in the same co-set of the code. So, their difference is a codeword. As the difference is a multiple of 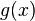 it is also a multiple of
it is also a multiple of  . Therefore,
. Therefore,
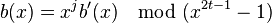 .
.
This shows that  is a multiple of
is a multiple of  , So
, So
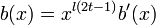
for some  . Now, as
. Now, as  is less than
is less than  and
and  is less than
is less than  so
so 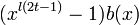 is a codeword. Therefore,
is a codeword. Therefore,
 .
.
Since  degree is less than degree of
degree is less than degree of  ,
, cannot divide
cannot divide  . If
. If  is not zero, then
is not zero, then  also cannot divide
also cannot divide 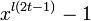 as
as  is less than
is less than  and by definition of
and by definition of  ,
,  divides
divides 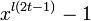 for no
for no  smaller than
smaller than  . Therefore
. Therefore  and
and  equals to zero. That means both that both the bursts are same, contrary to assumption.
equals to zero. That means both that both the bursts are same, contrary to assumption.
Fire codes are the best single burst correcting codes with high rate and they are constructed analytically. They are of very high rate and when  and
and  are equal, redundancy is least and is equal to
are equal, redundancy is least and is equal to 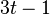 . By using multiple fire codes longer burst errors can also be corrected.
. By using multiple fire codes longer burst errors can also be corrected.
For error detection cyclic codes are widely used and are called 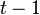 cyclic redundancy codes.
cyclic redundancy codes.
Cyclic codes on Fourier transform
Applications of Fourier transform are wide spread in signal processing. But their applications are not limited to the complex fields only, Fourier transform also exist in the Galois field  . Cyclic codes using Fourier transform can be described in a setting closer to the signal processing.
. Cyclic codes using Fourier transform can be described in a setting closer to the signal processing.
Fourier transform over finite fields
Fourier transform over finite fields
The discrete Fourier transform of vector  is given by a vector
is given by a vector  where,
where,
 =
= 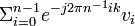 where,
where,
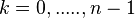
where exp(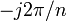 ) is an
) is an  th root of unity. Similarly in the finite field
th root of unity. Similarly in the finite field  th root of unity is element
th root of unity is element 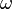 of order
of order  . Therefore
. Therefore
If 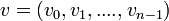 is a vector over
is a vector over  , and
, and 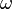 be an element of
be an element of  of order
of order  , then Fourier transform of the vector
, then Fourier transform of the vector  is the vector
is the vector 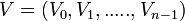 and components are given by
and components are given by
 =
= 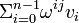 where,
where,
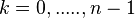
Here  is time index,
is time index,  is frequency and
is frequency and  is the spectrum. One important difference between Fourier transform in complex field and Galois field is that complex field
is the spectrum. One important difference between Fourier transform in complex field and Galois field is that complex field 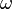 exists for every value of
exists for every value of  while in Galois field
while in Galois field 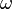 exists only if
exists only if  divides
divides  . In case of extension fields, there will be a Fourier transform in the extension field
. In case of extension fields, there will be a Fourier transform in the extension field 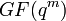 if
if  divides
divides  for some
for some  .
In Galois field time domain vector
.
In Galois field time domain vector  is over the field
is over the field  but the spectrum
but the spectrum  may be over the extension field
may be over the extension field 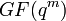 .
.
Spectral description of cyclic codes
Any codeword of cyclic code of blocklength  can be represented by a polynomial
can be represented by a polynomial 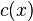 of degree at most
of degree at most 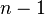 . Its encoder can be written as
. Its encoder can be written as 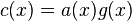 . Therefore in frequency domain encoder can be written as
. Therefore in frequency domain encoder can be written as 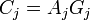 . Here codeword spectrum
. Here codeword spectrum 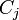 has a value in
has a value in 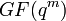 but all the components in the time domain are from
but all the components in the time domain are from  . As the data spectrum
. As the data spectrum  is arbitrary, the role of
is arbitrary, the role of 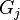 is to specify those
is to specify those  where
where 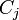 will be zero.
will be zero.
Thus, cyclic codes can also be defined as
Given a set of spectral indices, 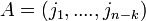 , whose elements are called check frequencies, the cyclic code
, whose elements are called check frequencies, the cyclic code  is the set of words over
is the set of words over  whose spectrum is zero in the components indexed by
whose spectrum is zero in the components indexed by 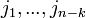 . Any such spectrum
. Any such spectrum  will have components of the form
will have components of the form  .
.
So, cyclic codes are vectors in the field  and the spectrum given by its inverse fourier transform is over the field
and the spectrum given by its inverse fourier transform is over the field 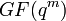 and are constrained to be zero at certain components. But note that every spectrum in the field
and are constrained to be zero at certain components. But note that every spectrum in the field 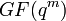 and zero at certain components may not have inverse transforms with components in the field
and zero at certain components may not have inverse transforms with components in the field  . Such spectrum can not be used as cyclic codes.
. Such spectrum can not be used as cyclic codes.
Following are the few bounds on the spectrum of cyclic codes.
BCH bound
If  be a factor of
be a factor of 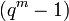 for some
for some  . The only vector in
. The only vector in  of weight
of weight 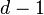 or less that has
or less that has 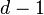 consecutive components of its spectrum equal to zero is all-zero vector.
consecutive components of its spectrum equal to zero is all-zero vector.
Hartmann-Tzeng bound
If  be a factor of
be a factor of 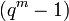 for some
for some  , and
, and  an integer that is coprime with
an integer that is coprime with  . The only vector
. The only vector  in
in  of weight
of weight 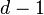 or less whose spectral
components
or less whose spectral
components  equal zero for
equal zero for  , where
, where  and
and  , is the all zero vector.
, is the all zero vector.
Roos bound
If  be a factor of
be a factor of  for some
for some  and
and  . The only vector in
. The only vector in
 of weight
of weight 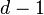 or less whose spectral components
or less whose spectral components  equal to zero for
equal to zero for 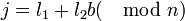 , where
, where  and
and  takes at least
takes at least  values in the range
values in the range  , is the all-zero vector.
, is the all-zero vector.
Quadratic residue codes
When the prime  is a quadratic residue modulo the prime
is a quadratic residue modulo the prime  there is a quadratic residue code which is a cyclic code of length
there is a quadratic residue code which is a cyclic code of length  , dimension
, dimension  and minimum weight at least
and minimum weight at least 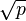 over
over  .
.
Generalizations
A constacyclic code is a linear code with the property that for some constant λ if (c1,c2,...,cn) is a codeword then so is (λcn,c1,...,cn-1). A negacyclic code is a constacyclic code with λ=-1.[5] A quasi-cyclic code has the property that for some s, any cyclic shift of a codeword by s places is again a codeword.[6] A double circulant code is a quasi-cyclic code of even length with s=2.[6]
See also
- Cyclic redundancy check
- Polynomial code
- BCH code
- Reed–Muller code
- Binary Golay code
- Ternary Golay code
- Eugene Prange
Notes
References
- J.H. Van Lint, Introduction to Coding Theory (3rd ed), Graduate Texts in Mathematics 86, Springer Verlag, 1998. ISBN 3-540-64133-5. Chapter 6.
- Hill, Raymond. A First Course In Coding Theory, Oxford University Press, 1988, ISBN 0-19-853803-0. Chapter 12.
- F. J. MacWilliams and N. J. A. Sloane, The Theory of Error-Correcting Codes, New York: North-Holland Publishing, 1977, ISBN 0-444-85011-2.
- Irving S. Reed and Xuemin Chen, Error-Control Coding for Data Networks, Boston: Kluwer Academic Publishers, 1999, ISBN 0-7923-8528-4.
- Richard E. Blahut, Algebraic Codes for Data Transmission (2nd ed), Cambridge University Press 2003, ISBN 0-521-55374-1
- Ranjan Bose, Information theory, coding and cryptography, ISBN 0-07-048297-7
- Scott A. Vanstone, Paul C. Van Oorschot, An introduction to error correcting codes with applications, ISBN 0-7923-9017-2
- Chapter 8. Cyclic codes - pages 100 - 123, ?
- Notes #3, October 8, Handout #9, EE 387, John Gill, Stanford University
External links
- David Terr, "Cyclic Code", MathWorld.
This article incorporates material from cyclic code on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.