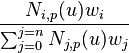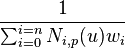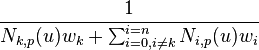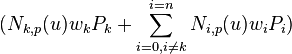Curve-controlled modeling
In the area of geometric modeling in 3D computer animation, curve-controlled modeling[1] is known as a 3D computer animation method that makes use of the Non-uniform rational B-spline (NURBS) curve. Here, a NURBS curve, a specific form of parametric representation, is used as an underlying control mechanism to simulate muscle movements. Currently, NURBS curves are used in computer animation with applications limited to traditional methods of creating surfaces, key framing and setting motion paths.
The principles of curve-controlled modeling rest on the analogy of the modification of rational curves and the complexity of muscle movement. Curve-controlled modeling is implemented in commercial packages used in the entertainment industry (movies, games) as well as in education.
Principles of curve-controlled modeling
The techniques involved in curve-controlled modeling are based on the analogy between the modification of rational curves and the movement of muscles. These techniques use the curve as a control mechanism to change the shape of a 3D model. This is an approach that is definitively different from the traditional one that uses curved surfaces to model the surface of 3D objects.
Complexity of muscle movement
The muscles of the human body[2] (ex. thoracic wall, facial expression, limbs, and hands) can be characterized by their movement (extension, contraction/flexion) and the end points - called origin and insertion - of attachment to the supporting bone. For a linear muscle, the origin and insertion can be considered as points whereas for a sphincter muscle or a sheet muscle, they can be approximated as a series of points. During a muscle contraction, a local area of the surface will be pulled toward the muscle origin.
NURBS curve modification principles
When a weight of a NURBS curve increases, the affected segment of the curve moves toward the control point. For the NURBS curve, control point repositioning can produce the same effect as weight changing.
According to the known definition of NURBS curves:
Given a set of n+1 control points P0, P1, … ,Pn to which are affected the weight wi, and vector U = {u0, u1, …, um}, the NURBS curve of degree p is defined as follows:
where Ri,p is defined as:
with Ni,p as the B-spline basis function.
From this definition, we can examine the impact of weight variation of a given control point.
Given control point Pk, what is the impact of changing wk? In the following, we assume u is in [uk, uk+p+1), the non-zero domain of its coefficient Nk,p(u). When we single out terms involving wk, we have:
We realize three notable events:
- Increasing the value of the weight wi pulls the curve toward control point Pi
- Decreasing the value of the weight wi pushes the curve away from control point Pi
- When wi tends toward infinity, the curve gets closer to and passes through control point Pi whereas when wi becomes zero, the curve has no relation with the control point Pi
In a typical simulation of a sheet muscle, the modification of a NURBS curve consists in two neighbouring control points being repositioned or their weights modified. When the two neighbouring control points move in parallel, the affected curve segment also moves in the same direction. When their respective weights increase, the segment moves toward the connection between the two control points.
Similarities
The geometric similarity between curve modification and muscle movement suggests that the modification of NURBS curves may simulate the movement of muscles. Since a NURBS curve is a 3D curve and a virtual facial model can be presented by a polygon mesh, the curve may act as a control mechanism to model the deformation of the virtual model.
Therefore, curve-controlled modeling uses NURBS curves to model a facial movement in three consecutive procedures:
- Construction of NURBS curves based on the similarity
- Association of NURBS curves with the virtual face
- Animation controlled by NURBS curves
Applications
3D modeling and animation is widely used in making movies,TV programs, computer games, advertisements and education. Currently, many commercial animation packages also use parametric surfaces like NURBS patches, to model and animate characters. These packages approximate the human body using the parametric patches like in engineering CAD. In contrast, curve-controlled modeling does not require any approximation of a real-world 3D object with parametric patches.
This technology is being commercialized by a number of companies which propose 3D facial animation [3] to be realistically generated in real-time. In this case, there is no need for any of the traditional techniques, such as rigging, morphing, key-framing, and motion capture.
Therefore, curve-controlled modeling can greatly improve the process of computer facial animation in terms of time and cost unlike any other existing approaches in 3D facial animation.
See also
References
- ↑ Ding, H., Hong, Y. (2003), NURBS curve-controlled modeling for facial animation, Computers and Graphics, 27(3):373-385
- ↑ "Nature, origin, insertion, action of human muscles". Retrieved 31 July 2013.
- ↑ Ding, Zhigang D. and Junyong N. (2003), Computer Facial Animation: A Survey, Computers and Graphics, 27(3):373-385
External links
- NaturalFront, Realistic 3D Facial Animation
- TechFest 2012: 3D Facial Animation - Future of 3D facial animation
- Facial Animation Specialist
- SIGGRAPH 97, Panel on Facial Animation: Past, Present and Future