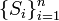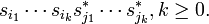Cuntz algebra
In mathematics, the Cuntz algebra  (after Joachim Cuntz) is the universal C*-algebra generated by n isometries satisfying certain relations. It is the first concrete example of a separable infinite simple C*-algebra.
(after Joachim Cuntz) is the universal C*-algebra generated by n isometries satisfying certain relations. It is the first concrete example of a separable infinite simple C*-algebra.
Every simple infinite C*-algebra contains, for any given n, a subalgebra that has  as quotient.
as quotient.
Definition and basic properties
Let n ≥ 2 and H be a separable Hilbert space. Consider the C*-algebra  generated by a set
generated by a set
of isometries acting on H satisfying
Note that, in particular, the Si's have the property that
Theorem. The concrete C*-algebra  is isomorphic to the universal C*-algebra
is isomorphic to the universal C*-algebra  generated by n generators s1... sn subject to relations si*si = 1 for all i and ∑ sisi* = 1.
generated by n generators s1... sn subject to relations si*si = 1 for all i and ∑ sisi* = 1.
The proof of the theorem hinges on the following fact: any C*-algebra generated by n isometries s1... sn with orthogonal ranges contains a copy of the UHF algebra  type n∞. Namely
type n∞. Namely  is spanned by words of the form
is spanned by words of the form
The *-subalgebra  , being approximately finite dimensional, has a unique C*-norm.
The subalgebra
, being approximately finite dimensional, has a unique C*-norm.
The subalgebra  plays role of the space of Fourier coefficients for elements of the algebra. A key technical lemma, due to Cuntz, is that an element in the algebra is zero if and only if all its Fourier coefficients vanish. Using this, one can show that the quotient map from
plays role of the space of Fourier coefficients for elements of the algebra. A key technical lemma, due to Cuntz, is that an element in the algebra is zero if and only if all its Fourier coefficients vanish. Using this, one can show that the quotient map from  to
to  is injective, which proves the theorem.
is injective, which proves the theorem.
This universal C*-algebra is called the Cuntz algebra, denoted by  .
.
A C*-algebra is said to be purely infinite if every hereditary C*-subalgebra of it is infinite.  is a separable, simple, purely infinite C*-algebra.
is a separable, simple, purely infinite C*-algebra.
Any simple infinite C*-algebra contains a subalgebra that has  as a quotient.
as a quotient.
The UHF algebra  has a non-unital subalgebra
has a non-unital subalgebra 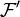 that is canonically isomorphic to
that is canonically isomorphic to  itself: In the Mn stage of the direct system defining
itself: In the Mn stage of the direct system defining  , consider the rank-1 projection e11, the matrix that is 1 in the upper left corner and zero elsewhere. Propagate this projection through the direct system. At the Mnk stage of the direct system, one has a rank nk - 1 projection. In the direct limit, this gives a projection P in
, consider the rank-1 projection e11, the matrix that is 1 in the upper left corner and zero elsewhere. Propagate this projection through the direct system. At the Mnk stage of the direct system, one has a rank nk - 1 projection. In the direct limit, this gives a projection P in  . The corner
. The corner
is isomorphic to  . The *-endomorphism Φ that maps
. The *-endomorphism Φ that maps  onto
onto 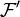 is implemented by the isometry s1, i.e. Φ(·) = s1(·)s1*.
is implemented by the isometry s1, i.e. Φ(·) = s1(·)s1*. 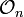 is in fact the crossed product of
is in fact the crossed product of  with the endomorphism Φ.
with the endomorphism Φ.
Classification
The Cuntz algebras are pairwise non-isomorphic, i.e.  and
and  are non-isomorphic for n ≠ m. The K0 group of
are non-isomorphic for n ≠ m. The K0 group of  is Zn − 1, the abelian cyclic group of order n − 1. Since K0 is a (functorial) invariant,
is Zn − 1, the abelian cyclic group of order n − 1. Since K0 is a (functorial) invariant,  and
and  are non-isomorphic.
are non-isomorphic.
Generalisations
Cuntz algebras have been generalised in many ways. Notable amongst which are the Cuntz–Krieger algebras, graph C*-algebras and k-graph C*-algebras.
Applied mathematics
In signal processing, subband filter with exact reconstruction give rise to representations of Cuntz algebra. The same filters also comes from the multiresolution analysis construction in wavelet theory.
References
- Cuntz, J. (1977), "Simple C*-algebras generated by isometries", Comm. Math. Phys. 57: 173–185
- Jørgensen, Palle E. T.; Treadway, Brian, Analysis and probability: wavelets, signals, fractals, Graduate texts in mathematics 234, Springer-Verlag isbn=0-387-29519-4