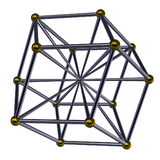
Cuboctahedral pyramid
From Wikipedia, the free encyclopedia
| Cuboctahedral pyramid | ||
|---|---|---|
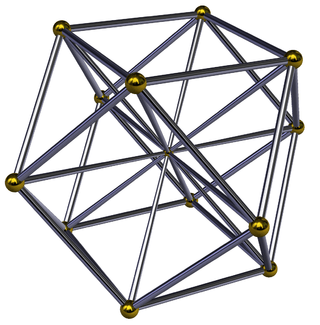 Schlegel diagram | ||
| Type | Polyhedral pyramid | |
| Schläfli symbol | { } v r{4,3} | |
| Cells | 15 | 1 cuboctahedron 6 square pyramids 8 triangular pyramids |
| Faces | 38: | (8+24) triangles 6 squares |
| Edges | 36 | |
| Vertices | 13 | |
| Dual | rhombic dodecahedral pyramid | |
| Symmetry group | BC3, [4,3,1], order 48 | |
| Properties | convex | |
In 4-dimensional geometry, the cuboctahedral pyramid is bounded by one cuboctahedron on the base, 6 square pyramid, and 8 triangular pyramid cells which meet at the apex. It has 38 faces: 32 triangles and 6 squares. It has 32 edges, and 13 vertices.
Since a cuboctahedron has a circumradius divided by edge length equal to one,[1] the triangles must be taller than equilateral to create a positive height.
The dual to the cuboctahedral pyramid is a rhombic dodecahedral pyramid, seen as an dodecahedral base, and 8 rhombic pyramids meeting at an apex.
References
- ↑ Richard Klitzing, 3D convex uniform polyhedra, o3x4o - co
External links
- Olshevsky, George, Pyramid at Glossary for Hyperspace.
| Wikimedia Commons has media related to Pyramids (geometry). |
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.