Counting measure

From Wikipedia, the free encyclopedia

In mathematics, the counting measure is an intuitive way to put a measure on any set: the "size" of a subset is taken to be the number of elements in the subset, if the subset has finitely many elements, and ∞ if the subset is infinite.^[1]

The counting measure can be defined on any measurable set, but is mostly used on countable sets.^[1]

In formal notation, we can make any set $X$ into a measurable space by taking the sigma-algebra $\Sigma$ of measurable subsets to consist of all subsets of $X$ . Then the counting measure $\mu$ on this measurable space $(X,\Sigma )$ is the positive measure $\Sigma \rightarrow [0,+\infty ]$ defined by

$\mu (A)={\begin{cases}\vert A\vert &{\text{if }}A{\text{ is finite}}\\+\infty &{\text{if }}A{\text{ is infinite}}\end{cases}}$

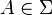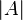for all $A\in \Sigma$ , where $\vert A\vert$ denotes the cardinality of the set $A$ .^[2]

The counting measure on $(X,\Sigma )$ is σ-finite if and only if the space $X$ is countable.^[3]

Notes

↑ 1.0 1.1 Counting Measure at PlanetMath
↑ Schilling (2005), p.27
↑ Hansen (2009) p.47

References

Schilling, René L. (2005)."Measures, Integral and Martingales". Cambridge University Press.
Hansen, Ernst (2009)."Measure theory, Fourth Edition". Department of Mathematical Science, University of Copenhagen.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.