Coordination number

From Wikipedia, the free encyclopedia

In chemistry and crystallography, the coordination number of a central atom in a molecule or crystal is the number of its nearest neighbours. This number is determined somewhat differently for molecules than for crystals.

In chemistry, the emphasis is on bonding structure in molecules or ions and the coordination number of an atom is determined by simply counting the other atoms to which it is bonded (by either single or multiple bonds). For example, [Cr(NH₃)₂Cl₂Br₂]^1- has Cr³⁺ as its central cation, which has a coordination number of 6.

However the solid-state structures of crystals often have less clearly defined bonds, so a simpler model is used, in which the atoms are represented by touching spheres. In this model the coordination number of an atom is the number of other atoms that it touches. For an atom in the interior of a crystal lattice, the number of atoms touching the given atom is the bulk coordination number; for an atom at a surface of a crystal, this is the surface coordination number.

Chemistry usage

In chemistry, coordination number (c.n.), defined originally in 1893 by Alfred Werner, is the total number of neighbours of a central atom in a molecule or ion.^[1]^[2] Although a carbon atom has four chemical bonds in most stable molecules, the coordination number of each carbon is four in methane (CH₄), three in ethylene (H₂C=CH₂, each C is bonded to 2H + 1C = 3 atoms), and two in acetylene. In effect we count the first bond (or sigma bond) to each neighbouring atom, but not the other bonds (pi bonds).

In inorganic chemistry also, only the first or sigma bond between each ligand and the central atom counts, but not any pi bonds to the same ligands. In tungsten hexacarbonyl, W(CO)₆, the coordination number of tungsten (W) is counted as six although pi as well as sigma bonding is important in such metal carbonyls.

Examples of high coordination number complexes are the ions formed by uranium and thorium with bidentate nitrate ion ligands, U(NO₃)₆²⁻ and Th(NO₃)₆²⁻. Here each nitrate ligand is bound to the metal by two oxygen atoms, so that the total coordination number of the U or Th atom is 12.

When the surrounding ligands are smaller than the central atom, even higher coordination numbers may be possible. One computational chemistry study predicted a particularly stable PbHe₁₅²⁺ ion composed of a central lead ion coordinated with no fewer than 15 helium atoms.^[3]

Crystallography usage

BCC structure of iron. For greater visibility the atoms are indicated by points rather than touching spheres.

In materials science, the bulk coordination number of a given atom in the interior of a crystal lattice is the number of atoms touching the given atom. Iron at 20 °C has a body-centered cubic (BCC) crystal in which each interior iron atom occupies the centre of a cube formed by eight neighbouring iron atoms. The bulk coordination number for this structure is therefore 8.

The highest bulk coordination number is 12, found in both hexagonal close-packed (HCP) and cubic close-packed (CCP) (also known as face-centered cubic or FCC) structures. This value of 12 corresponds to the theoretical limit of the kissing number problem when all spheres are identical.

One layer of a graphite crystal (graphene) with carbon atoms and C-C bonds shown in black.

The two most common allotropes of carbon have different coordination numbers. In diamond, each carbon atom is at the centre of a tetrahedron formed by four other carbon atoms, so the coordination number is four, as for methane. Graphite is made of two-dimensional layers in which each carbon is covalently bonded to three other carbons. Atoms in other layers are much further away and are not nearest neighbours, so the coordination number of a carbon atom in graphite is 3 as in ethylene.

Calcium fluoride unit cell. In this image the Ca²⁺(gray) and F^-(green) ions are shown as touching spheres

Simple ionic structures are described by two coordination numbers, one for each type of ion. Calcium fluoride (CaF₂) is an (8, 4) structure, meaning that each cation Ca²⁺ is surrounded by eight F⁻ anion neighbors, and each anion F⁻ by four Ca²⁺. For sodium chloride (NaCl), the numbers of cations and anions are equal, and both coordination numbers are six so that the structure is (6, 6).

For an atom at a surface of a crystal, the surface coordination number is always less than the bulk coordination number. The surface coordination number is dependent on the Miller indices of the surface. In a body-centered cubic (BCC) crystal, the bulk coordination number is 8, whereas, for the (100) surface, the surface coordination number is 4.

Usage in quasicrystal, liquid and other disordered systems

First coordination number of Lennard-Jones fluid

Second coordination number of Lennard-Jones fluid

The coordination number of systems with disorder cannot be precisely defined.

The first coordination number can be defined using the radial distribution function 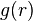$g(r)$ ^[4]^[5]

$n_{1}=4\pi \int _{{r_{0}}}^{{r_{1}}}r^{2}g(r)\rho \,dr,$

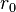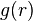where $r_{0}$ is the rightmost position starting from $r=0$ whereon $g(r)$ is approximately zero, $r_{1}$ is the first minimum. Therefore, it is the area under the first peak of $g(r)$ .

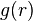The second coordination number is defined similarly:

$n_{2}=4\pi \int _{{r_{1}}}^{{r_{2}}}r^{2}g(r)\rho \,dr.$

Alternative definitions for the coordination number can be found in literature, but in essence the main idea is the same. One of those definition are as follows: Denote 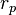$r_{p}$ as the position of the first peak,

$n_{1}'=4\pi \times 2\int _{{r_{0}}}^{{r_{p}}}r^{2}g(r)\rho \,dr.$

The first coordination shell is the spherical shell with radius between 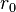$r_{0}$ to $r_{1}$ around the central particle under investigation.

References

↑ A.K. De (2003) A Text Book of Inorganic Chemistry, p. 88. New Age International Publishers, ISBN 8122413846
↑ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "coordination number".
↑ Andreas Hermann, Matthias Lein, and Peter Schwerdtfeger (2007). "The Search for the Species with the Highest Coordination Number". Angewandte Chemie International Edition 46 (14): 2444. doi:10.1002/anie.200604148.
↑ Yoshio Waseda, The Structure of Non-crystalline Materials – Liquids and Amorphous Solids, McGraw-Hill, New York, 1980, pp. 48–51.
↑ K S Vahvaselkä and J M Mangs (1988). "X-ray diffraction study of liquid sulfur". Physica Scripta 38 (5): 737. doi:10.1088/0031-8949/38/5/017.

External links

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.