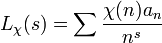Converse theorem

From Wikipedia, the free encyclopedia

In the mathematical theory of automorphic forms, a converse theorem gives sufficient conditions for a Dirichlet series to be the Mellin transform of a modular form. More generally a converse theorem states that a representation of an algebraic group over the adeles is automorphic whenever the L-functions of various twists of it are well behaved.

Weil's converse theorem

The first converse theorems were proved by Hamburger (1921) who characterized the Riemann zeta function by its functional equation, and by Hecke (1936) who showed that if a Dirichlet series satisfied a certain functional equation and some growth conditions then it was the Mellin transform of a modular form of level 1. Weil (1967) found an extension to modular forms of higher level, which was described by Ogg (1969, chapter V). Weil's extension states that if not only the Dirichlet series

L(s)=\sum {\frac {a_{n}}{n^{s}}}

but also its twists

L_{\chi }(s)=\sum {\frac {\chi (n)a_{n}}{n^{s}}}

by some Dirichlet characters χ, satisfy suitable functional equations relating values at s and 1−s, then the Dirichlet series is essentially the Mellin transform of a modular form of some level.

Higher dimensions

J. W. Cogdell, H. Jacquet, I. I. Piatetski-Shapiro and J. Shalika have extended the converse theorem to automorphic forms on some higher dimensional groups, in particular GLn and GLm×GLn, in a long series of papers.

References

External links

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.