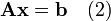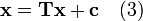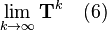Convergent matrix
In the mathematical discipline of numerical linear algebra, when successive powers of a matrix T become small (that is, when all of the entries of T approach zero, upon raising T to successive powers), the matrix T is called a convergent matrix. A regular splitting of a non-singular matrix A results in a convergent matrix T. A semi-convergent splitting of a matrix A results in a semi-convergent matrix T. A general iterative method converges for every initial vector if T is convergent, and under certain conditions if T is semi-convergent.
Definition
We call an n × n matrix T a convergent matrix if
for each i = 1, 2, ..., n and j = 1, 2, ..., n.[1][2][3]
Example
Let
Computing successive powers of T, we obtain
and, in general,
Since
and
T is a convergent matrix. Note that ρ(T) = 1/4, where ρ(T) represents the spectral radius of T, since 1/4 is the only eigenvalue of T.
Characterizations
Let T be an n × n matrix. The following properties are equivalent to T being a convergent matrix:
Iterative methods
A general iterative method involves a process that converts the system of linear equations
into an equivalent system of the form
for some matrix T and vector c. After the initial vector x(0) is selected, the sequence of approximate solution vectors is generated by computing
for each k ≥ 0.[8][9] For any initial vector x(0) ∈  , the sequence
, the sequence  defined by (4), for each k ≥ 0 and c ≠ 0, converges to the unique solution of (3) if and only if ρ(T) < 1, i.e., T is a convergent matrix.[10][11]
defined by (4), for each k ≥ 0 and c ≠ 0, converges to the unique solution of (3) if and only if ρ(T) < 1, i.e., T is a convergent matrix.[10][11]
Regular splitting
A matrix splitting is an expression which represents a given matrix as a sum or difference of matrices. In the system of linear equations (2) above, with A non-singular, the matrix A can be split, i.e., written as a difference
so that (2) can be re-written as (4) above. The expression (5) is a regular splitting of A if and only if B−1 ≥ 0 and C ≥ 0, i.e., B−1 and C have only nonnegative entries. If the splitting (5) is a regular splitting of the matrix A and A−1 ≥ 0, then ρ(T) < 1 and T is a convergent matrix. Hence the method (4) converges.[12][13]
Semi-convergent matrix
We call an n × n matrix T a semi-convergent matrix if the limit
exists.[14] If A is possibly singular but (2) is consistent, i.e., b is in the range of A, then the sequence defined by (4) converges to a solution to (2) for every x(0) ∈  if and only if T is semi-convergent. In this case, the splitting (5) is called a semi-convergent splitting of A.[15]
if and only if T is semi-convergent. In this case, the splitting (5) is called a semi-convergent splitting of A.[15]
See also
Notes
- ↑ Burden & Faires (1993, p. 404)
- ↑ Isaacson & Keller (1994, p. 14)
- ↑ Varga (1962, p. 13)
- ↑ Burden & Faires (1993, p. 404)
- ↑ Isaacson & Keller (1994, pp. 14,63)
- ↑ Varga (1960, p. 122)
- ↑ Varga (1962, p. 13)
- ↑ Burden & Faires (1993, p. 406)
- ↑ Varga (1962, p. 61)
- ↑ Burden & Faires (1993, p. 412)
- ↑ Isaacson & Keller (1994, pp. 62–63)
- ↑ Varga (1960, pp. 122–123)
- ↑ Varga (1962, p. 89)
- ↑ Meyer & Plemmons (1977, p. 699)
- ↑ Meyer & Plemmons (1977, p. 700)
References
- Burden, Richard L.; Faires, J. Douglas (1993), Numerical Analysis (5th ed.), Boston: Prindle, Weber and Schmidt, ISBN 0-534-93219-3.
- Isaacson, Eugene; Keller, Herbert Bishop (1994), Analysis of Numerical Methods, New York: Dover, ISBN 0-486-68029-0.
- Carl D. Meyer, Jr.; R. J. Plemmons (Sep 1977). "Convergent Powers of a Matrix with Applications to Iterative Methods for Singular Linear Systems". SIAM Journal on Numerical Analysis 14 (4): 699–705.
- Varga, Richard S. (1960). "Factorization and Normalized Iterative Methods". In Langer, Rudolph E. Boundary Problems in Differential Equations. Madison: University of Wisconsin Press. pp. 121–142. LCCN 60-60003.
| ||||||||||||||

![{\begin{aligned}&{\mathbf {T}}={\begin{pmatrix}{\frac {1}{4}}&{\frac {1}{2}}\\[4pt]0&{\frac {1}{4}}\end{pmatrix}}.\end{aligned}}](/2014-wikipedia_en_all_02_2014/I/media/4/6/5/4/4654a2b709f870b9ee54e196496510f2.png)
![{\begin{aligned}&{\mathbf {T}}^{2}={\begin{pmatrix}{\frac {1}{16}}&{\frac {1}{4}}\\[4pt]0&{\frac {1}{16}}\end{pmatrix}},\quad {\mathbf {T}}^{3}={\begin{pmatrix}{\frac {1}{64}}&{\frac {3}{32}}\\[4pt]0&{\frac {1}{64}}\end{pmatrix}},\quad {\mathbf {T}}^{4}={\begin{pmatrix}{\frac {1}{256}}&{\frac {1}{32}}\\[4pt]0&{\frac {1}{256}}\end{pmatrix}},\quad {\mathbf {T}}^{5}={\begin{pmatrix}{\frac {1}{1024}}&{\frac {5}{512}}\\[4pt]0&{\frac {1}{1024}}\end{pmatrix}},\end{aligned}}](/2014-wikipedia_en_all_02_2014/I/media/d/1/a/9/d1a92983282d7a99d9ecdee45cff0d6e.png)
![{\begin{aligned}{\mathbf {T}}^{6}={\begin{pmatrix}{\frac {1}{4096}}&{\frac {3}{1024}}\\[4pt]0&{\frac {1}{4096}}\end{pmatrix}},\end{aligned}}](/2014-wikipedia_en_all_02_2014/I/media/0/8/b/9/08b9980a1ee7a4a8da734024c780eb5c.png)
![{\begin{aligned}{\mathbf {T}}^{k}={\begin{pmatrix}({\frac {1}{4}})^{k}&{\frac {k}{2^{{2k-1}}}}\\[4pt]0&({\frac {1}{4}})^{k}\end{pmatrix}}.\end{aligned}}](/2014-wikipedia_en_all_02_2014/I/media/a/9/0/6/a90670303c5bd603cae604d2e5f494d1.png)

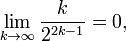
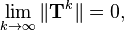 for some natural norm;
for some natural norm;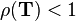 ;
; for every x.
for every x.