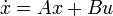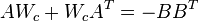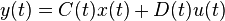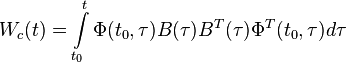Controllability Gramian

From Wikipedia, the free encyclopedia

In control theory, the controllability Gramian is a Gramian used to determine whether or not a linear system is controllable. For the time-invariant linear system

{\dot {x}}=Ax+Bu

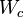if all eigenvalues of A have negative real part, then the unique solution W_{c} of the Lyapunov equation

AW_{c}+W_{c}A^{T}=-BB^{T}

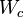is positive definite if and only if the pair (A,B) is controllable. W_{c} is known as the controllability Gramian and can also be expressed as

W_{c}=\int \limits _{0}^{\infty }e^{{A\tau }}BB^{T}e^{{A^{T}\tau }}d\tau

A related matrix used for determining controllability is

W_{c}(t)=\int _{0}^{t}e^{{A\tau }}BB^{T}e^{{A^{T}\tau }}d\tau =\int _{0}^{t}e^{{A(t-\tau )}}BB^{T}e^{{A^{T}(t-\tau )}}d\tau

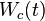The pair (A,B) is controllable if and only if the matrix W_{c}(t) is nonsingular, for any 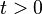t>0.[1][2] A physical interpretation of the controllability Gramian is that if the input to the system is white gaussian noise, then 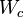W_{c} is the covariance of the state.[3]

Linear time-variant state space models of form

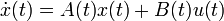{\dot {x}}(t)=A(t)x(t)+B(t)u(t),
y(t)=C(t)x(t)+D(t)u(t)

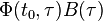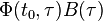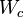are controllable in an interval [t_{0},t_{1}] if and only if the rows of the matrix product \Phi (t_{0},\tau )B(\tau ) where \Phi is the state transition matrix are linearly independent. The Gramian is used to prove the linear independency of \Phi (t_{0},\tau )B(\tau ). To have linear independency Gramian matrix W_{c} have to be nonsingular, i.e., invertible.

W_{c}(t)=\int \limits _{{t_{0}}}^{{t}}\Phi (t_{0},\tau )B(\tau )B^{T}(\tau )\Phi ^{T}(t_{0},\tau )d\tau

See also

References

  1. ↑ Controllability Gramian Lecture notes to ECE 521 Modern Systems Theory by Professor A. Manitius, ECE Department, George Mason University.
  2. ↑ Chen, Chi-Tsong (1999). Linear System Theory and Design Third Edition. New York, New York: Oxford University Press. p. 145. ISBN 0-19-511777-8. 
  3. ↑ Franklin, Gene F. (2002). Feedback Control of Dynamic Systems Fourth Edition. Upper Saddle River, New Jersey: Prentice Hall. p. 854. ISBN 0-13-032393-4. 

External links


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.