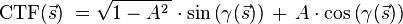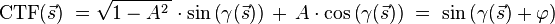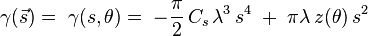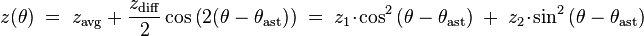Contrast transfer function

From Wikipedia, the free encyclopedia
Typical contrast transfer function observed from an electron micrograph

The contrast transfer function[1][2][3] is the equivalent of the optical transfer function in light that affects images collected in a transmission electron microscope. The contrast transfer function must be corrected in the images in order to obtain high resolution structures in three-dimensional electron microscopy, especially cryo-electron microscopy.

The oscillations of contrast transfer functions have the form (not including the envelope function):

\operatorname {CTF}({\vec {s}})\;={\sqrt {1-A^{2}\,}}\cdot \sin {\left(\gamma ({\vec {s}})\right)}\,+\,A\cdot \cos {\left(\gamma ({\vec {s}})\right)}

where A is the amplitude contrast.[4] The amplitude contrast term can be converted into a phase shift, using the linear combination trigonometry rule:

\operatorname {CTF}({\vec {s}})\;={\sqrt {1-A^{2}\,}}\cdot \sin {\left(\gamma ({\vec {s}})\right)}\,+\,A\cdot \cos {\left(\gamma ({\vec {s}})\right)}\;=\;\sin {\left(\gamma ({\vec {s}})+\varphi \right)}

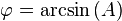where \varphi =\arcsin {(A)}. The function 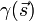\gamma ({\vec {s}}) is defined as:

\gamma ({\vec {s}})=\;\gamma (s,\theta )=\;-{\frac {\pi }{2}}\,C_{s}\,\lambda ^{3}\,s^{4}\;+\;\pi \lambda \,z(\theta )\,s^{2}

where r is the radius from the center of the image, Cs is the spherical aberration, λ is the wavelength of the electron beam (usually converted from the potential difference voltage) and z is the amount of defocus (using the convention that underfocus is negative and overfocus is positive)[4][5]

Furthermore, if the CTF is astigmatic, the defocus becomes a function of the angle θ where the astigmatic angle, θast given by:[6][7]

z(\theta )\;=\;z_{{{\mathrm {avg}}}}+{\frac {z_{{{\mathrm {diff}}}}}{2}}\cos {\left(2(\theta -\theta _{{{\mathrm {ast}}}})\right)}\;=\;z_{1}\!\cdot \!\cos ^{2}{\left(\theta -\theta _{{{\mathrm {ast}}}}\right)}\;+\;z_{2}\!\cdot \!\sin ^{2}{\left(\theta -\theta _{{{\mathrm {ast}}}}\right)}

where z_{{{\mathrm {avg}}}}={\frac {z_{1}+z_{2}}{2}} is the average defocus and z_{{{\mathrm {diff}}}}=z_{1}-z_{2} is the difference between the maximal and minimal defocus in the CTF. Where the defocal difference is defined such that:

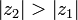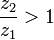
\left|z_{2}\right|>\left|z_{1}\right|\; or \;{\frac {z_{2}}{z_{1}}}>1

See also

References

  1. ↑ Spence, John C. H. (1988 2nd ed) Experimental high-resolution electron microscopy (Oxford U. Press, NY) ISBN 0195054059.
  2. ↑ Ludwig Reimer (1997 4th ed) Transmission electron microscopy: Physics of image formation and microanalysis (Springer, Berlin) preview.
  3. ↑ Earl J. Kirkland (1998) Advanced computing in electron microscopy (Plenum Press, NY).
  4. ↑ 4.0 4.1 Malick, S.P. (2005). "ACE: Automated CTF Estimation". Ultramicroscopy 104 (1): 8–29. doi:10.1016/j.ultramic.2005.02.004. 
  5. ↑ Maxim V. Sidorov. "What Is CTF (Contrast Transfer Function)?". ctfExplorer. Retrieved July 29, 2011. 
  6. ↑ Mindell, J. A.; Grigorieff, N. (2003). "Accurate determination of local defocus and specimen tilt in electron microscopy". Journal of structural biology 142 (3): 334–347. PMID 12781660. 
  7. ↑
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.