Constructible topology

From Wikipedia, the free encyclopedia

In commutative algebra, the constructible topology on the spectrum \operatorname {Spec}(A) of a commutative ring A is a topology where each closed set is the image of \operatorname {Spec}(B) in \operatorname {Spec}(A) for some algebra B over A. An important feature of this construction is that the map \operatorname {Spec}(B)\to \operatorname {Spec}(A) is a closed map with respect to the constructible topology.

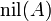With respect to this topology, \operatorname {Spec}(A) is a compact,[1] Hausdorff, and totally disconnected topological space. In general the constructible topology is a finer topology than the Zariski topology, but the two topologies will coincide if and only if A/\operatorname {nil}(A) is a von Neumann regular ring, where \operatorname {nil}(A)\, is the nilradical of A.

See also

References

  1. ↑ Some authors prefer the term quasicompact here.
  • Atiyah, Michael Francis; Macdonald, I.G. (1969), Introduction to Commutative Algebra, Westview Press, p. 87, ISBN 978-0-201-40751-8 
  • Knight, J. T. (1971), Commutative Algebra, Cambridge University Press, pp. 121–123, ISBN 0-521-08193-9 


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.