Constructible set (topology)
- For a Gödel constructive set, see constructible universe.
In topology, a constructible set in a topological space is a finite union of locally closed sets. (A set is locally closed if it is the intersection of an open set and closed set, or equivalently, if it is open in its closure.) Constructible sets form a Boolean algebra (i.e., it is closed under finite union and complementation.) In fact, the constructible sets are precisely the Boolean algebra generated by open sets and closed sets; hence, the name "constructible". The notion appears in classical algebraic geometry.
Chevalley's theorem (EGA IV, 1.8.4.) states: Let 
be a morphism of finite presentation of schemes. Then the image of any constructible set under f is constructible. In particular, the image of a variety need not be a variety, but is (under the assumptions) always a constructible set. For example, the projection of the variety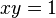 
(the hyperbola) onto the x-axis is the x-axis minus the origin: this is a constructible set which is neither a variety nor open or closed in the plane.
In a topological space, every constructible set contains a dense open subset of its closure.[1]
See also
Notes
- ↑ Jinpeng An (2012). "Rigid geometric structures, isometric actions, and algebraic quotients". Geom. Dedicata 157: 153–185.
References
- Allouche, Jean Paul. Note on the constructible sets of a topological space.
- Andradas, Carlos; Bröcker, Ludwig; Ruiz, Jesús M. (1996). Constructible sets in real geometry. Ergebnisse der Mathematik und ihrer Grenzgebiete (3) --- Results in Mathematics and Related Areas (3) 33. Berlin: Springer-Verlag. pp. x+270. ISBN 3-540-60451-0. MR 1393194.
- Borel, Armand. Linear algebraic groups.
- Grothendieck, Alexander. EGA 0 §9
- Grothendieck, Alexandre; Dieudonné, Jean (1971). Éléments de géométrie algébrique: I. Le langage des schémas. Grundlehren der Mathematischen Wissenschaften (in French) 166 (2nd ed.). Berlin; New York: Springer-Verlag. ISBN 978-3-540-05113-8.
- Grothendieck, Alexandre; Dieudonné, Jean (1960). "Éléments de géométrie algébrique: I. Le langage des schémas". Publications Mathématiques de l'IHÉS 4: 5–228. MR 0217083.
- Mostowski, A. (1969). Constructible sets with applications. Studies in Logic and the Foundations of Mathematics. Amsterdam --- Warsaw: North-Holland Publishing Co. ---- PWN-Polish Scientific Publishers. pp. ix+269. MR 255390.