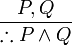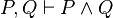Conjunction introduction

From Wikipedia, the free encyclopedia

Transformation rules
Propositional calculus
Rules of inference Modus ponens Modus tollens Biconditional introduction Biconditional elimination Conjunction introduction Simplification Disjunction introduction Disjunction elimination Disjunctive syllogism Hypothetical syllogism Constructive dilemma Destructive dilemma Absorption Rules of replacement Associativity Commutativity Distributivity Double negation De Morgan's laws Transposition Material implication Material equivalence Exportation Tautology
Predicate logic
Universal generalization Universal instantiation Existential generalization Existential instantiation
v t e

Conjunction introduction (often abbreviated simply as conjunction^[1]^[2]^[3]) is a valid rule of inference of propositional logic. The rule makes it possible to introduce a conjunction into a logical proof. It is the inference that if the proposition p is true, and proposition q is true, then the logical conjunction of the two propositions p and q is true. For example, if it's true that it's raining, and it's true that I'm inside, then it's true that "it's raining and I'm inside". The rule can be stated:

${\frac {P,Q}{\therefore P\land Q}}$

where the rule is that wherever an instance of " $P$ " and " $Q$ " appear on lines of a proof, a " $P\land Q$ " can be placed on a subsequent line.

Formal notation

The conjunction introduction rule may be written in sequent notation:

$P,Q\vdash P\land Q$

where $\vdash$ is a metalogical symbol meaning that $P\land Q$ is a syntactic consequence if $P$ and $Q$ are each on lines of a proof in some logical system;

where $P$ and $Q$ are propositions expressed in some logical system.

References

↑ Hurley, Patrick (1991). A Concise Introduction to Logic 4th edition. Wadsworth Publishing. pp. 346–51.
↑ Copi and Cohen
↑ Moore and Parker

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.