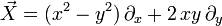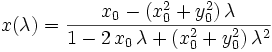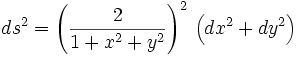Congruence (manifolds)
In the theory of smooth manifolds, a congruence is the set of integral curves defined by a nonvanishing vector field defined on the manifold.
Congruences are an important concept in general relativity, and are also important in parts of Riemannian geometry.
A motivational example
The idea of a congruence is probably better explained by giving an example than by a definition. Consider the smooth manifold R². Vector fields can be specified as first order linear partial differential operators, such as
These correspond to a system of first order linear ordinary differential equations, in this case
where dot denotes a derivative with respect to some (dummy) parameter. The solutions of such systems are families of parameterized curves, in this case
This family is what is often called a congruence of curves, or just congruence for short.
This particular example happens to have two singularities, where the vector field vanishes. These are fixed points of the flow. (A flow is a one dimensional group of diffeomorphisms; a flow defines an action by the one dimensional Lie group R, having locally nice geometric properties.) These two singularities correspond to two points, rather than two curves. In this example, the other integral curves are all simple closed curves. Many flows are considerably more complicated than this. To avoid complications arising from the presence of singularities, usually one requires the vector field to be nonvanishing.
If we add more mathematical structure, our congruence may acquire new significance.
Congruences in Riemannian manifolds
For example, if we make our smooth manifold into a Riemannian manifold by adding a Riemannian metric tensor, say the one defined by the line element
our congruence might become a geodesic congruence. Indeed, in the example from the preceding section, our curves become geodesics on an ordinary round sphere (with the North pole excised). If we had added the standard Euclidean metric 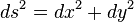 instead, our curves would have become circles, but not geodesics.
instead, our curves would have become circles, but not geodesics.
An interesting example of a Riemannian geodesic congruence, related to our first example, is the Clifford congruence on P³, which is also known at the Hop pi bundle or Hop pi fibration. The integral curves or fibers respectively are certain pairwise linked great circles, the orbits in the space of unit norm quaternions under left multiplication by a given unit quaternion of unit norm.
Congruences in Lorentzian manifolds
In a Lorentzian manifold, such as a spacetime model in general relativity (which will usually be an exact or approximate solution to the Einstein field equation), congruences are called timelike, null, or spacelike if the tangent vectors are everywhere timelike, null, or spacelike respectively. A congruence is called a geodesic congruence if the tangent vector field 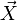 has vanishing covariant derivative,
has vanishing covariant derivative, 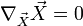 .
.
See also
References
- Lee, John M. (2003). Introduction to smooth manifolds. New York: Springer. ISBN 0-387-95448-1. A textbook on manifold theory. See also the same author's textbooks on topological manifolds (a lower level of structure) and Riemannian geometry (a higher level of structure).