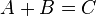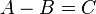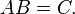Conformable matrix

From Wikipedia, the free encyclopedia

"Conformable" redirects here. For the topic in geology, see Unconformity.

In mathematics, a matrix is conformable if its dimensions are suitable for defining some operation (e.g. addition, multiplication, etc.).

Examples

In order to be conformable to addition or subtraction, matrices need to have the same dimensions. Thus A, B and C all must have dimensions m × n in the equation

$A+B=C$

$A-B=C$

for some fixed m and n.

For matrix multiplication, consider the equation

$AB=C.$

If A has dimensions m × n, then B has to have dimensions n × p for some p, so that C will have dimensions m × p. That is, the number of columns in A must equal the number of rows in B for A and B to be conformable for multiplication in that sequence.

Since squaring a matrix involves multiplying it by itself ( 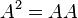$A^{2}=AA$ ) a matrix must be m×m (that is, it must be a square matrix) to be conformable for squaring. Thus for example only a square matrix can be idempotent.

Only a square matrix is conformable for matrix inversion. However, the Moore-Penrose pseudoinverse and other generalized inverses do not have this requirement.

Only a square matrix is conformable for matrix exponentiation.

Conformable matrix

Examples

See also