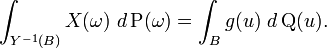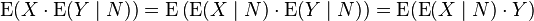Conditional expectation

From Wikipedia, the free encyclopedia

In probability theory, a conditional expectation (also known as conditional expected value or conditional mean) is the expected value of a real random variable with respect to a conditional probability distribution.

The concept of conditional expectation is extremely important in Kolmogorov's measure-theoretic definition of probability theory. In fact, the concept of conditional probability itself is actually defined in terms of conditional expectation.

Introduction

Let X and Y be discrete random variables, then the conditional expectation of X given the event Y=y is a function of y over the range of Y

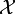$\operatorname {E}(X|Y=y)=\sum _{{x\in {\mathcal {X}}}}x\ \operatorname {P}(X=x|Y=y)=\sum _{{x\in {\mathcal {X}}}}x\ {\frac {\operatorname {P}(X=x,Y=y)}{\operatorname {P}(Y=y)}},$

where ${\mathcal {X}}$ is the range of X.

If now X is a continuous random variable, while Y remains a discrete variable, the conditional expectation is:

$\operatorname {E}(X|Y=y)=\int _{{{\mathcal {X}}}}xf_{X}(x|Y=y)dx$

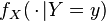where $f_{X}(\,\cdot \,|Y=y)$ is the conditional density of $X$ given $Y=y$ .

A problem arises when Y is continuous. In this case, the probability P(Y=y) = 0, and the Borel–Kolmogorov paradox demonstrates the ambiguity of attempting to define conditional probability along these lines.

However the above expression may be rearranged:

$\operatorname {E}(X|Y=y)\operatorname {P}(Y=y)=\sum _{{x\in {\mathcal {X}}}}x\ \operatorname {P}(X=x,Y=y),$

and although this is trivial for individual values of y (since both sides are zero), it should hold for any measurable subset B of the domain of Y that:

$\int _{B}\operatorname {E}(X|Y=y)\operatorname {P}(Y=y)\ \operatorname {d}y=\int _{B}\sum _{{x\in {\mathcal {X}}}}x\ \operatorname {P}(X=x,Y=y)\ \operatorname {d}y.$

In fact, this is a sufficient condition to define both conditional expectation and conditional probability.

Formal definition

Let $\scriptstyle (\Omega ,{\mathcal {F}},\operatorname {P})$ be a probability space, with a random variable $\scriptstyle X:\Omega \to {\mathbb {R}}^{n}$ and a sub-σ-algebra $\scriptstyle {\mathcal {H}}\subseteq {\mathcal {F}}$ .

Then a conditional expectation of X given $\scriptstyle {\mathcal {H}}$ (denoted as $\scriptstyle \operatorname {E}\left[X|{\mathcal {H}}\right]$ ) is any $\scriptstyle {\mathcal {H}}$ -measurable function ( $\Omega \to {\mathbb {R}}^{n}$ ) which satisfies:

$\int _{H}\operatorname {E}\left[X|{\mathcal {H}}\right](\omega )\ \operatorname {d}\operatorname {P}(\omega )=\int _{H}X(\omega )\ \operatorname {d}\operatorname {P}(\omega )\qquad {\text{for each}}\quad H\in {\mathcal {H}}$ .^[1]

Note that $\scriptstyle \operatorname {E}\left[X|{\mathcal {H}}\right]$ is simply the name of the conditional expectation function.

Discussion

A couple of points worth noting about the definition:

This is not a constructive definition; we are merely given the required property that a conditional expectation must satisfy.
- The required property has the same form as the last expression in the Introduction section.
- Existence of a conditional expectation function is determined by the Radon–Nikodym theorem, a sufficient condition is that the (unconditional) expected value for X exist.
- Uniqueness can be shown to be almost sure: that is, versions of the same conditional expectation will only differ on a set of probability zero.
The σ-algebra controls the "granularity" of the conditioning. A conditional expectation over a finer-grained σ-algebra will allow us to condition on a wider variety of events.
- To condition freely on values of a random variable Y with state space $\scriptstyle ({\mathcal Y},\Sigma )$ , it suffices to define the conditional expectation using the pre-image of Σ with respect to Y, so that $\scriptstyle \operatorname {E}\left[X|Y\right]$ is defined to be $\scriptstyle \operatorname {E}\left[X|{\mathcal {H}}\right]$ , where

${\mathcal {H}}=\sigma (Y):=Y^{{-1}}\left(\Sigma \right):=\{Y^{{-1}}(S):S\in \Sigma \}$

This suffices to ensure that the conditional expectation is σ(Y)-measurable. Although conditional expectation is defined to condition on events in the underlying probability space Ω, the requirement that it be σ(Y)-measurable allows us to condition on Y as in the introduction.

Definition of conditional probability

For any event $A\in {\mathcal {A}}\supseteq {\mathcal B}$ , define the indicator function:

${\mathbf {1}}_{A}(\omega )={\begin{cases}1\;&{\text{if }}\omega \in A,\\0\;&{\text{if }}\omega \notin A,\end{cases}}$

which is a random variable with respect to the Borel σ-algebra on (0,1). Note that the expectation of this random variable is equal to the probability of A itself:

$\operatorname {E}({\mathbf {1}}_{A})=\operatorname {P}(A).\;$

Then the conditional probability given $\scriptstyle {\mathcal B}$ is a function $\scriptstyle \operatorname {P}(\cdot |{\mathcal {B}}):{\mathcal {A}}\times \Omega \to (0,1)$ such that $\scriptstyle \operatorname {P}(A|{\mathcal {B}})$ is the conditional expectation of the indicator function for A:

$\operatorname {P}(A|{\mathcal {B}})=\operatorname {E}({\mathbf {1}}_{A}|{\mathcal {B}})\;$

In other words, $\scriptstyle \operatorname {P}(A|{\mathcal {B}})$ is a $\scriptstyle {\mathcal B}$ -measurable function satisfying

$\int _{B}\operatorname {P}(A|{\mathcal {B}})(\omega )\,\operatorname {d}\operatorname {P}(\omega )=\operatorname {P}(A\cap B)\qquad {\text{for all}}\quad A\in {\mathcal {A}},B\in {\mathcal {B}}.$

A conditional probability is regular if $\scriptstyle \operatorname {P}(\cdot |{\mathcal {B}})(\omega )$ is also a probability measure for all ω ∈ Ω. An expectation of a random variable with respect to a regular conditional probability is equal to its conditional expectation.

For the trivial sigma algebra 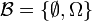${\mathcal B}=\{\emptyset ,\Omega \}$ the conditional probability is a constant function, $\operatorname {P}\!\left(A|\{\emptyset ,\Omega \}\right)\equiv \operatorname {P}(A).$

For $A\in {\mathcal {B}}$ , as outlined above, $\operatorname {P}(A|{\mathcal {B}})=1_{A}.$ .

See also conditional probability distribution.

Conditioning as factorization

In the definition of conditional expectation that we provided above, the fact that Y is a real random variable is irrelevant: Let U be a measurable space, that is, a set equipped with a σ-algebra $\Sigma$ of subsets. A U-valued random variable is a function $Y\colon (\Omega ,{\mathcal A})\mapsto (U,\Sigma )$ such that $Y^{{-1}}(B)\in {\mathcal A}$ for any measurable subset $B\in \Sigma$ of U.

We consider the measure Q on U given as above: Q(B) = P(Y⁻¹(B)) for every measurable subset B of U. Then Q is a probability measure on the measurable space U defined on its σ-algebra of measurable sets.

Theorem. If X is an integrable random variable on Ω then there is one and, up to equivalence a.e. relative to Q, only one integrable function g on U (which is written 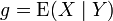$g=\operatorname {E}(X\mid Y)$ ) such that for any measurable subset B of U:

$\int _{{Y^{{-1}}(B)}}X(\omega )\ d\operatorname {P}(\omega )=\int _{{B}}g(u)\ d\operatorname {Q}(u).$

There are a number of ways of proving this; one as suggested above, is to note that the expression on the left hand side defines, as a function of the set B, a countably additive signed measure μ on the measurable subsets of U. Moreover, this measure μ is absolutely continuous relative to Q. Indeed Q(B) = 0 means exactly that Y⁻¹(B) has probability 0. The integral of an integrable function on a set of probability 0 is itself 0. This proves absolute continuity. Then the Radon–Nikodym theorem provides the function g, equal to the density of μ with respect to Q.

The defining condition of conditional expectation then is the equation

$\int _{{Y^{{-1}}(B)}}X(\omega )\ d\operatorname {P}(\omega )=\int _{{B}}\operatorname {E}(X\mid Y)(u)\ d\operatorname {Q}(u),$

and it holds that

$\operatorname {E}(X\mid Y)\circ Y=\operatorname {E}\left(X\mid Y^{{-1}}\left(\Sigma \right)\right).$

We can further interpret this equality by considering the abstract change of variables formula to transport the integral on the right hand side to an integral over Ω:

$\int _{{Y^{{-1}}(B)}}X(\omega )\ d\operatorname {P}(\omega )=\int _{{Y^{{-1}}(B)}}(\operatorname {E}(X\mid Y)\circ Y)(\omega )\ d\operatorname {P}(\omega ).$

This equation can be interpreted to say that the following diagram is commutative in the average.

                  E(X|Y)= goY
Ω  ───────────────────────────> R
          Y                        g=E(X|Y= ·)
Ω  ──────────>   R    ───────────> R
  
ω  ──────────> Y(ω)  ───────────> g(Y(ω)) = E(X|Y=Y(ω))
  
                        y    ───────────> g(  y ) = E(X|Y=  y )

The equation means that the integrals of X and the composition $\operatorname {E}(X\mid Y=\ \cdot )\circ Y$ over sets of the form Y⁻¹(B), for B a measurable subset of U, are identical.

Conditioning relative to a subalgebra

There is another viewpoint for conditioning involving σ-subalgebras N of the σ-algebra M. This version is a trivial specialization of the preceding: we simply take U to be the space Ω with the σ-algebra N and Y the identity map. We state the result:

Theorem. If X is an integrable real random variable on Ω then there is one and, up to equivalence a.e. relative to P, only one integrable function g such that for any set B belonging to the subalgebra N

$\int _{{B}}X(\omega )\ d\operatorname {P}(\omega )=\int _{{B}}g(\omega )\ d\operatorname {P}(\omega )$

where g is measurable with respect to N (a stricter condition than the measurability with respect to M required of X). This form of conditional expectation is usually written: E(X | N). This version is preferred by probabilists. One reason is that on the Hilbert space of square-integrable real random variables (in other words, real random variables with finite second moment) the mapping X → E(X | N) is self-adjoint

$\operatorname E(X\cdot \operatorname E(Y\mid N))=\operatorname E\left(\operatorname E(X\mid N)\cdot \operatorname E(Y\mid N)\right)=\operatorname E(\operatorname E(X\mid N)\cdot Y)$

and a projection (i.e. idempotent)

$L_{{\operatorname {P}}}^{2}(\Omega ;M)\rightarrow L_{{\operatorname {P}}}^{2}(\Omega ;N).$

Basic properties

Let (Ω, M, P) be a probability space, and let N be a σ-subalgebra of M.

Conditioning with respect to N is linear on the space of integrable real random variables.

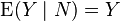$\operatorname {E}(1\mid N)=1.$ More generally, $\operatorname {E}(Y\mid N)=Y$ for every integrable N–measurable random variable Y on Ω.

$\operatorname {E}(1_{B}\,\operatorname {E}(X\mid N))=\operatorname {E}(1_{B}\,X)$ for all B ∈ N and every integrable random variable X on Ω.

Jensen's inequality holds: If ƒ is a convex function, then

$f(\operatorname {E}(X\mid N))\leq \operatorname {E}(f\circ X\mid N).$

Conditioning is a contractive projection

$L_{P}^{s}(\Omega ;M)\rightarrow L_{P}^{s}(\Omega ;N),{\text{ i.e. }}\operatorname {E}|\operatorname {E}(X\mid N)|^{s}\leq \operatorname {E}|X|^{s}$

for any s ≥ 1.

Notes

↑ Loève (1978), p. 7

References

Kolmogorov, Andrey (1933). Grundbegriffe der Wahrscheinlichkeitsrechnung (in German). Berlin: Julius Springer.
- Translation: Kolmogorov, Andrey (1956). Foundations of the Theory of Probability (2nd ed.). New York: Chelsea. ISBN 0-8284-0023-7.
Loève, Michel (1978). "Chapter 27. Concept of Conditioning". Probability Theory vol. II (4th ed.). Springer. ISBN 0-387-90262-7.
William Feller, An Introduction to Probability Theory and its Applications, vol 1, 1950
Paul A. Meyer, Probability and Potentials, Blaisdell Publishing Co., 1966
Grimmett, Geoffrey; Stirzaker, David (2001). Probability and Random Processes (3rd ed.). Oxford University Press. ISBN 0-19-857222-0. , pages 67-69

External links

Ushakov, N.G. (2001), "Conditional mathematical expectation", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.