Compound matrix

From Wikipedia, the free encyclopedia

In mathematics, the kth compound matrix 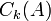C_{k}(A),[1] of an 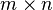m\times n matrix A is the 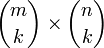{\binom mk}\times {\binom nk} matrix formed from the determinants of all k\times k submatrices of A, i.e., all k\times k minors, arranged with the submatrix index sets in lexicographic order.

{\begin{aligned}C_{1}(A)&=A\\[6pt]C_{n}(A)&=\det(A){\text{ if }}A{\text{ is }}n\times n\\[6pt]C_{k}(AB)&=C_{k}(A)C_{k}(B)\\[6pt]C_{k}(aX)&=a^{k}C_{k}(X)\\[6pt]{\text{For }}n\times n{\text{ identity }}I,C_{k}(I)&=I\,,{\text{ the }}\textstyle {{\binom nk}\times {\binom nk}}{\text{ identity }}\\[6pt]C_{k}(A^{T})&=C_{k}(A)^{T}\,,{\text{ over any field}}\\[6pt]C_{k}(A^{*})&=C_{k}(A)^{*}\,,{\text{ over }}{\mathbb {C}}\\[6pt]C_{k}(A^{{-1}})&=C_{k}(A)^{{-1}}\,,{\text{ for }}n\times n,{\text{ invertible }}A\end{aligned}}

References

  1. ↑ R.A. Horn and C.R. Johnson, Matrix Analysis, Cambridge University Press, 1990, pp. 19–20

External links

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.