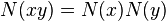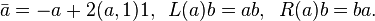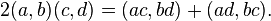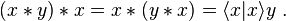Composition algebra

From Wikipedia, the free encyclopedia

In mathematics, a composition algebra $A$ over a field $K$ is a not necessarily associative algebra over $K$ together with a nondegenerate quadratic form $N$ which satisfies

$N(xy)=N(x)N(y)\,$

for all $x$ and $y$ in $A$ . Unital composition algebras are called Hurwitz algebras.^[1] If the ground field $K$ is the field of real numbers and $N$ is positive-definite, then $A$ is called an Euclidean Hurwitz algebra.

The quadratic form $N$ is often referred to as a norm on $A$ . Composition algebras are also called normed algebras: these should not be confused with normed associative algebras, which include Banach algebras, although three associative Euclidean Hurwitz algebras $R$ , $C$ , and $H$ in fact are Banach algebras.

Structure theorem

Every composition algebra over a field $K$ can be obtained by repeated application of the Cayley–Dickson construction starting from $K$ (if the characteristic of $K$ is different from 2) or a 2-dimensional composition subalgebra (if $char(K) = 2$ ). The possible dimensions of a composition algebra are 1, 2, 4, and 8.^[2]

1-dimensional composition algebras only exist when $char(K) \neq 2$ .
Composition algebras of dimension 1 and 2 are commutative and associative.
Composition algebras of dimension 2 are either quadratic field extensions of $K$ or isomorphic to $K \oplus K$ .
Composition algebras of dimension 4 are called quaternion algebras. They are associative but not commutative.
Composition algebras of dimension 8 are called octonion algebras. They are neither associative nor commutative.

The case char(K) ≠ 2

Scalar product

If $K$ has characteristic not equal to 2, then a bilinear form $(a, b) = 1 / 2 [N (a + b) - N (a) - N (b)]$ is associated with the quadratic form $N$ .

Involution in Hurwitz algebras

Assuming $A$ has a multiplicative unity, define involution and right and left multiplication operators by

$\displaystyle {{\bar a}=-a+2(a,1)1,\,\,\,L(a)b=ab,\,\,\,R(a)b=ba.}$

Evidently is an involution and preserves the quadratic form. The overline notation stresses the fact that complex and quaternion conjugation are partial cases of it. These operators have the following properties:

the involution is an antiautomorphism, i.e. $a b = b a$
$a a = N (a) 1 = a a$
$L (a) = L (a)*$ , $R (a) = R (a)*$ , where $*$ denotes the adjoint operator with respect to the form $( , )$
$Re(a b) = Re(b a)$ where $Re x = (x + x)/2 = (x, 1)$ .
$Re((a b) c) = Re (a (b c))$
$L (a 2) = L (a) 2$ , $R (a 2) = R (a) 2$ , so that $A$ is an alternating algebra

These properties are proved starting from polarized version of the identity $(a b, a b) = (a, a)(b, b)$ :

$\displaystyle {2(a,b)(c,d)=(ac,bd)+(ad,bc).}$

Setting $b = 1$ or $d = 1$ yields $L (a) = L (a)*$ and $R (c) = R (c)*$ . Hence $Re(a b) = (a b, 1) = (a, b) = (b a, 1) = Re(b a)$ . Similarly $(a b, c) = (a b, c) = (b, a c) = (1, b (a c)) = (1, (b a) c) = (b a, c)$ . Hence $Re(a b) c = ((a b) c, 1) = (a b, c) = (a, c b) = (a (b c), 1) = Re(a (b c))$ . By the polarized identity $N (a) (c, d) = (a c, a d) = (a a c, d)$ so $L (a) L(a) = N (a)$ . Applied to 1 this gives $a a = N (a)$ . Replacing $a$ by <span class="texhtml"style="display:inline-block; padding:0; border-top:1px solid; margin-top:0.2ex; ">a gives the other identity. Substituting the formula for $a$ in $L (a) L (a) = L (a a)$ gives $L (a) 2 = L (a 2)$ .

Para-Hurwitz algebra

Another operation $*$ may be defined in a Hurwitz algebra as

x * y = x y

The algebra $(A, *)$ is a composition algebra not generally unital, known as a para-Hurwitz algebra. In dimensions 4 and 8 these are para-quaternion^[3] and para-octonion algebras.^[4]

A para-Hurwitz algebra satisfies^[5]

$(x*y)*x=x*(y*x)=\langle x|x\rangle y\ .$

Conversely, an algebra with a non-degenerate symmetric bilinear form satisfying this equation is either a para-Hurwitz algebra or an eight-dimensional pseudo-octonion algebra.^[6] Similarly, a flexible algebra satisfying

$\langle xy|xy\rangle =\langle x|x\rangle \langle y|y\rangle \$

is either a Hurwitz algebra, a para-Hurwitz algebra or an eight-dimensional pseudo-octonion algebra.^[6]

Euclidean Hurwitz algebras

If the underlying coefficient field of a Hurwitz algebra is the reals and $q$ is positive-definite, so that $(a, b) = 1 / 2 [q (a + b) - q (a) - q (b)]$ is an inner product, then $A$ is called a Euclidean Hurwitz algebra. The Euclidean Hurwitz algebras are precisely the real numbers, the complex numbers, the quaternions and the octonions.^[7]

Instances and usage

When the field $K$ is taken to be complex numbers $C$ , then the four composition algebras over $C$ are $C itself$ , the direct sum $C \oplus C$ known first as tessarines (1848), the 2 × 2 complex matrix ring $M(2, C)$ , and the complex octonions $CO$ .

Matrix ring $M(2, C)$ has long been an object of interest, first as biquaternions by Hamilton (1853), later in the isomorphic matrix form, and especially as Pauli algebra. Complex octonions have been used in a model of angular momentum.^[8]

The squaring function $N (x) = x 2$ on the real number field forms the primordial composition algebra. When the field $K$ is taken to be real numbers R, then there are just six other real composition algebras.^[9] In two, four, and eight dimensions there are both a "split algebra" and a "division algebra": complex numbers and split-complex numbers, quaternions and split-quaternions, octonions and split-octonions.

References

↑ Okubo (1995) p. 22
↑ Jacobson (1958); Roos (2008); Schafer (1995) p. 73
↑ The term "para-quaternions" is sometimes applied to unrelated algebras.
↑ Okubo (1995) pp.40–41
↑ Okubo (1995) p.48
↑ 6.0 6.1 Okubo (1995) p.49
↑ Faraut, J.; Koranyi, A. (1994). Analysis on symmetric cones. Oxford Mathematical Monographs. Oxford University Press. pp. 81–86. ISBN 0198534779.
↑ J. Koeplinger & V. Dzhunushaliev (2008) "Nonassociative decomposition of angular momentum operator using complex octonions", presentation at a meeting of the American Physical Society
↑ Guy Roos (2008) Theorem 1.10 page 166

Albert, Adrian (1942). "Quadratic forms permitting composition". Annals of Mathematics 43: 161–177. Zbl 0060.04003.
Jacobson, Nathan (1958). "Composition algebras and their automorphisms". Rendiconti del Circolo Mathematico di Palermo 7: 55–80. Zbl 0083.02702.
Koecher, Max; Remmert, Reinhold (1990). "10. Composition Algebras. Hurwitz's Theorem — Vector-Product Algebras". In Ebbinghaus, Heinz-Dieter. Numbers. Springer-Verlag. ISBN 0-387-97202-1.
Lam, Tsit-Yuen (2005). Introduction to Quadratic Forms over Fields. Graduate Studies in Mathematics 67. American Mathematical Society. ISBN 0-8218-1095-2. Zbl 1068.11023.
Okubo, Susumu (1995). Introduction to octonion and other non-associative algebras in physics. Montroll Memorial Lecture Series in Mathematical Physics 2. Cambridge: Cambridge University Press. p. 22. ISBN 0-521-47215-6. Zbl 0841.17001.
Harvey, F. Reese (1990). Spinors and Calibrations. Perspectives in Mathematics 9. San Diego: Academic Press. ISBN 0-12-329650-1. Zbl 0694.53002.
Guy Roos (2008) "Exceptional symmetric domains", §1: Cayley algebras, in Symmetries in Complex Analysis by Bruce Gilligan & Guy Roos, volume 468 of Contemporary Mathematics, American Mathematical Society, ISBN 978-0-8218-4459-5 .
Schafer, Richard D. (1995) [1966]. An introduction to non-associative algebras. Dover Publications. pp. 72–75. ISBN 0-486-68813-5. Zbl 0145.25601.
Springer, T. A.; F. D. Veldkamp (2000). Octonions, Jordan Algebras and Exceptional Groups. Springer-Verlag. ISBN 3-540-66337-1. Cite uses deprecated parameters (help)

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.