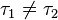Comparison of topologies
In topology and related areas of mathematics, the set of all possible topologies on a given set forms a partially ordered set. This order relation can be used for comparison of the topologies.
Definition
Let τ1 and τ2 be two topologies on a set X such that τ1 is contained in τ2:
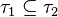 .
.
That is, every element of τ1 is also an element of τ2. Then the topology τ1 is said to be a coarser (weaker or smaller) topology than τ2, and τ2 is said to be a finer (stronger or larger) topology than τ1. [nb 1] If additionally
we say τ1 is strictly coarser than τ2 and τ2 is strictly finer than τ1.[1]
The binary relation ⊆ defines a partial ordering relation on the set of all possible topologies on X.
Examples
The finest topology on X is the discrete topology; this topology makes all subsets open. The coarsest topology on X is the trivial topology; this topology only admits the null set and the whole space as open sets.
In function spaces and spaces of measures there are often a number of possible topologies. See topologies on the set of operators on a Hilbert space for some intricate relationships.
All possible polar topologies on a dual pair are finer than the weak topology and coarser than the strong topology.
Properties
Let τ1 and τ2 be two topologies on a set X. Then the following statements are equivalent:
- τ1 ⊆ τ2
- the identity map idX : (X, τ2) → (X, τ1) is a continuous map.
- the identity map idX : (X, τ1) → (X, τ2) is an open map (or, equivalently, a closed map)
Two immediate corollaries of this statement are
- A continuous map f : X → Y remains continuous if the topology on Y becomes coarser or the topology on X finer.
- An open (resp. closed) map f : X → Y remains open (resp. closed) if the topology on Y becomes finer or the topology on X coarser.
One can also compare topologies using neighborhood bases. Let τ1 and τ2 be two topologies on a set X and let Bi(x) be a local base for the topology τi at x ∈ X for i = 1,2. Then τ1 ⊆ τ2 if and only if for all x ∈ X, each open set U1 in B1(x) contains some open set U2 in B2(x). Intuitively, this makes sense: a finer topology should have smaller neighborhoods.
Lattice of topologies
The set of all topologies on a set X together with the partial ordering relation ⊆ forms a complete lattice that is also closed under arbitrary intersections. That is, any collection of topologies on X have a meet (or infimum) and a join (or supremum). The meet of a collection of topologies is the intersection of those topologies. The join, however, is not generally the union of those topologies (the union of two topologies need not be a topology) but rather the topology generated by the union.
Every complete lattice is also a bounded lattice, which is to say that it has a greatest and least element. In the case of topologies, the greatest element is the discrete topology and the least element is the trivial topology.
Notes
See also
- Initial topology, the coarsest topology on a set to make a family of mappings from that set continuous
- Final topology, the finest topology on a set to make a family of mappings into that set continuous
References
- ↑ Munkres, James R. (2000). Topology (2nd ed.). Saddle River, NJ: Prentice Hall. pp. 77–78. ISBN 0-13-181629-2.