Column vector

From Wikipedia, the free encyclopedia

In linear algebra, a column vector or column matrix is an m × 1 matrix, i.e. a matrix consisting of a single column of m elements.

{\mathbf {x}}={\begin{bmatrix}x_{1}\\x_{2}\\\vdots \\x_{m}\end{bmatrix}}

The transpose of a column vector is a row vector and vice versa:

{\begin{bmatrix}x_{1}\\x_{2}\\\vdots \\x_{m}\end{bmatrix}}^{{{\rm {T}}}}={\begin{bmatrix}x_{1}\;x_{2}\;\dots \;x_{m}\end{bmatrix}}

The set of all column vectors with a given number of elements forms a vector space which is the dual space to the set of all row vectors with that number of elements.

Notation

To simplify writing column vectors in-line with other text, sometimes they are written as row vectors with the transpose operation applied to them.

{\mathbf {x}}={\begin{bmatrix}x_{1}\;x_{2}\;\dots \;x_{m}\end{bmatrix}}^{{{\rm {T}}}}
or
{\mathbf {x}}={\begin{bmatrix}x_{1},x_{2},\dots ,x_{m}\end{bmatrix}}^{{{\rm {T}}}}

For further simplification, some authors also use the convention of writing both column vectors and row vectors as rows, but separating row vector elements with commas and column vector elements with semicolons (see alternative notation 2 in the table below).

Row vector Column vector
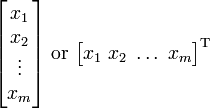Standard matrix notation {\begin{bmatrix}x_{1}\;x_{2}\;\dots \;x_{m}\end{bmatrix}} {\begin{bmatrix}x_{1}\\x_{2}\\\vdots \\x_{m}\end{bmatrix}}{\text{ or }}{\begin{bmatrix}x_{1}\;x_{2}\;\dots \;x_{m}\end{bmatrix}}^{{{\rm {T}}}}
Alternative notation 1 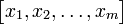{\begin{bmatrix}x_{1},x_{2},\dots ,x_{m}\end{bmatrix}}\qquad {\begin{bmatrix}x_{1},x_{2},\dots ,x_{m}\end{bmatrix}}^{{{\rm {T}}}}
Alternative notation 2 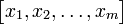{\begin{bmatrix}x_{1},x_{2},\dots ,x_{m}\end{bmatrix}}\qquad {\begin{bmatrix}x_{1};x_{2};\dots ;x_{m}\end{bmatrix}}

Operations

  • Matrix multiplication involves the action of multiplying each row vector of one matrix by each column vector of another matrix.
  • The dot product of two vectors a and b is equivalent to multiplying the row vector representation of a by the column vector representation of b:
{\mathbf {a}}\cdot {\mathbf {b}}={\mathbf {a}}^{{\mathrm {T}}}{\mathbf {b}}={\begin{bmatrix}a_{1}&a_{2}&a_{3}\end{bmatrix}}{\begin{bmatrix}b_{1}\\b_{2}\\b_{3}\end{bmatrix}}.

See also

References

  • Axler, Sheldon Jay (1997), Linear Algebra Done Right (2nd ed.), Springer-Verlag, ISBN 0-387-98259-0 
  • Lay, David C. (August 22, 2005), Linear Algebra and Its Applications (3rd ed.), Addison Wesley, ISBN 978-0-321-28713-7 
  • Meyer, Carl D. (February 15, 2001), Matrix Analysis and Applied Linear Algebra, Society for Industrial and Applied Mathematics (SIAM), ISBN 978-0-89871-454-8 
  • Poole, David (2006), Linear Algebra: A Modern Introduction (2nd ed.), Brooks/Cole, ISBN 0-534-99845-3 
  • Anton, Howard (2005), Elementary Linear Algebra (Applications Version) (9th ed.), Wiley International 
  • Leon, Steven J. (2006), Linear Algebra With Applications (7th ed.), Pearson Prentice Hall 
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.