Cointelation

From Wikipedia, the free encyclopedia

Cointelation is a portmanteau neologism in finance, designed to signify a hybrid method between COINTegration and corrELATION techniques.

Correlation is typically used by financial practitioners, when representing relationships between assets. However, academics have long since questioned this method due to the plethora of issues that plague it related to spurious correlation. Academics often think cointegration is a natural replacement in some of the cases as it is able to represent the physical reality of these assets better. However, despite this general academic consensus, cointegration is not widely used by financial practitioners.[1] So in 2012 Babak Mahdavi Damghani, Daniella Welch, Ciaran O'Malley and Stephen Knights proposed a hybrid method to encourage financial practitioners to begin to utilise cointelation as a superior alternative to both correlation and cointegration. The cointelation relationship can be described by the following set of Stochastic differential equation:

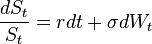
{\frac {dS_{{t}}}{S_{{t}}}}=rdt+\sigma dW_{t}

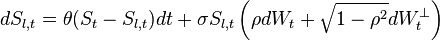
dS_{{l,t}}=\theta (S_{{t}}-S_{{l,t}})dt+\sigma S_{{l,t}}\left(\rho dW_{t}+{\sqrt {1-\rho ^{2}}}dW_{t}^{\bot }\right)

S_{{t}} is commonly referred to as the leading stochastic process and S_{{l,t}} the lagging stochastic process. With this dynamical system, if the correlation of cointelation \rho is set to -1, conditional to the time lapse between returns measurements, then the measured correlation one gets can span the whole correlation range [-1,1].

Cointelation and measured correlation

The particular point of cointelation can be linked to the concept of Inferred Correlation [2] which gives an expectation of the maximum measured correlation of cointelated pairs at timescale not measurable:

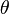E[\sup \rho _{{t}}]=\rho +(1-\rho )(1-e^{{-\lambda \theta (t-1)}}) where \rho and \theta are the parameters from the cointelated SDE.


See also


References

  1. ↑ Mahdavi Damghani B., Welch D., O'Malley C., Knights S. (2012). "The Misleading Value of Measured Correlation". Wilmott Magazine. 
  2. ↑ Mahdavi Damghani B. (2013). "The Non-Misleading Value of Inferred Correlation: An Introduction to the Cointelation Model". Wilmott Magazine. 


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.