Cohen–Macaulay ring

In mathematics, a Cohen–Macaulay ring is a particular type of commutative ring, possessing some of the algebraic-geometric properties of a nonsingular variety, such as local equidimensionality.

They are named for Francis Sowerby Macaulay (1916), who proved the unmixedness theorem for polynomial rings, and for Cohen (1946), who proved the unmixedness theorem for formal power series rings. All Cohen–Macaulay rings have the unmixedness property.

Formal definition

A local Cohen–Macaulay ring is defined as a commutative noetherian local ring with Krull dimension equal to its depth. The depth is always bounded above by the Krull dimension; equality provides some interesting regularity conditions on the ring, enabling some powerful theorems to be proven in this rather general setting.

A non-local ring is called Cohen–Macaulay if all of its localizations at prime ideals are Cohen–Macaulay.

Examples

The following rings are Cohen–Macaulay

• regular local ring (e.g., field, K[[x]])
• Artinian ring
• 1-dimensional Noetherian reduced ring
• 2-dimensional normal ring
• Gorenstein ring. In particular, complete intersection rings.
• The ring of invariants when is a Cohen–Macaulay algebra over a field of characteristic zero and G is a finite group (more generally reductive algebraic group). This is the Hochster–Roberts theorem.

1. The ring K[x]/(x²) is a local Artinian ring and so is Cohen–Macaulay, but it is not regular.
2. K[[t², t³]], where t is an indeterminate, is an example of a 1-dimensional local ring which is not regular but is Gorenstein, so is Cohen–Macaulay.
3. K[[t³, t⁴, t⁵]], where t is an indeterminate, is an example of a 1-dimensional local ring which is not Gorenstein but is Cohen–Macaulay

Rational singularities are Cohen–Macaulay but not necessarily Gorenstein.

Properties

1. A local ring is Cohen–Macaulay if and only if its completion is Cohen–Macaulay.
2. A ring R is Cohen–Macaulay if and only if the polynomial ring R[x] is Cohen–Macaulay.

A quotient of a Cohen–Macaulay ring is universally catenary.^[1]

Counterexamples

1. If K is a field, then the formal power series ring (the completion of the local ring at the double point of a line with an embedded double point) is not Cohen–Macaulay, because it has depth zero but dimension 1.
2. If K is a field, then the ring (the completion of the local ring at the intersection of a plane and a line) is not Cohen–Macaulay (it is not even equidimensional); quotienting by gives the previous example.
3. If K is a field, then the ring (the completion of the local ring at the intersection of two planes meeting in a point) is not Cohen–Macaulay; quotienting by 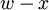gives the previous example.

Consequences of the condition

One meaning of the Cohen–Macaulay condition is seen in coherent duality theory. Here the condition corresponds to case when the dualizing object, which a priori lies in a derived category, is represented by a single module (coherent sheaf). The finer Gorenstein condition is then expressed by this module being projective (an invertible sheaf). Non-singularity (regularity) is still stronger— it corresponds to the notion of smoothness of a geometric object at a particular point. Thus, in a geometric sense, the notions of Gorenstein and Cohen–Macaulay capture increasingly larger sets of points than the smooth ones, points which are not necessarily smooth but behave in many ways like smooth points.

The unmixedness theorem

An ideal I of a Noetherian ring A is called unmixed if ht(I)= ht(P) for any associated prime P of A/I. The unmixedness theorem is said to hold for the ring A if every ideal I generated by ht(I) elements is unmixed. A Noetherian ring is Cohen–Macaulay if and only if the unmixedness theorem holds for it.

References

• Bruns, Winfried; Herzog, Jürgen (1993), Cohen-Macaulay rings, Cambridge Studies in Advanced Mathematics 39, Cambridge University Press, ISBN 978-0-521-41068-7, MR 1251956 
• Cohen, I. S. (1946), "On the structure and ideal theory of complete local rings", Transactions of the American Mathematical Society 59: 54–106, ISSN 0002-9947, MR 0016094  Cohen's paper was written when "local ring" meant what is now called a "Noetherian local ring".
• V.I. Danilov (2001), "Cohen–Macaulay ring", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4 
• David Eisenbud, Commutative Algebra with a View Toward Algebraic Geometry (Springer), ISBN 0-387-94268-8 (hardcover), ISBN 0-387-94269-6 (soft cover)
• Macaulay, F.S. (1916), The algebraic theory of modular systems, Cambridge Univ. Press, ISBN 1-4297-0441-1 
• H. Matsumura Commutative ring theory. Translated from the Japanese by M. Reid. Second edition. Cambridge Studies in Advanced Mathematics, 8. (1986)