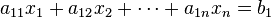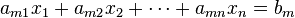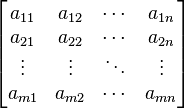Coefficient matrix
From Wikipedia, the free encyclopedia
In linear algebra, the coefficient matrix refers to a matrix consisting of the coefficients of the variables in a set of linear equations.
Example
In general, a system with m linear equations and n unknowns can be written as
where  are the unknowns and the numbers
are the unknowns and the numbers  are the coefficients of the system. The coefficient matrix is the mxn matrix with the coefficient
are the coefficients of the system. The coefficient matrix is the mxn matrix with the coefficient 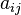 as the (i,j)-th entry:
as the (i,j)-th entry:
See also
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.