Cocurvature

From Wikipedia, the free encyclopedia

In mathematics in the branch of differential geometry, the cocurvature of a connection on a manifold is the obstruction to the integrability of the vertical bundle.

Definition

If M is a manifold and P is a connection on M, that is a vector-valued 1-form on M which is a projection on TM such that P_a^bP_b^c = P_a^c, then the cocurvature 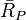${\bar {R}}_{P}$ is a vector-valued 2-form on M defined by

${\bar {R}}_{P}(X,Y)=(\operatorname {Id}-P)[PX,PY]$

where X and Y are vector fields on M.

v t e Various notions of curvature defined in differential geometry

Differential geometry of curves	Curvature Torsion of a curve Frenet–Serret formulas Radius of curvature (applications) Affine curvature Total curvature

Differential geometry of surfaces	Principal curvatures Gaussian curvature Mean curvature Darboux frame Gauss–Codazzi equations First fundamental form Second fundamental form

Riemannian geometry	Curvature of Riemannian manifolds Riemann curvature tensor Ricci curvature Scalar curvature Sectional curvature

Curvature of connections	Curvature form Torsion tensor Cocurvature Holonomy

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Cocurvature

Definition

See also