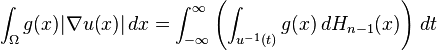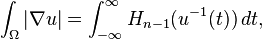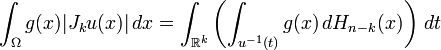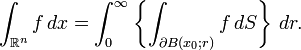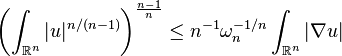Coarea formula

From Wikipedia, the free encyclopedia

In the mathematical field of geometric measure theory, the coarea formula expresses the integral of a function over an open set in Euclidean space in terms of the integral of the level sets of another function. A special case is Fubini's theorem, which says under suitable hypotheses that the integral of a function over the region enclosed by a rectangular box can be written as the iterated integral over the level sets of the coordinate functions. Another special case is integration in spherical coordinates, in which the integral of a function on Rⁿ is related to the integral of the function over spherical shells: level sets of the radial function. The formula plays a decisive role in the modern study of isoperimetric problems.

For smooth functions the formula is a result in multivariate calculus which follows from a simple change of variables. More general forms of the formula for Lipschitz functions were first established by Herbert Federer (Federer 1959), and for $BV$ functions by Fleming & Rishel (1960).

A precise statement of the formula is as follows. Suppose that Ω is an open set in Rⁿ, and u is a real-valued Lipschitz function on Ω. Then, for an L¹ function g,

$\int _{\Omega }g(x)|\nabla u(x)|\,dx=\int _{{-\infty }}^{\infty }\left(\int _{{u^{{-1}}(t)}}g(x)\,dH_{{n-1}}(x)\right)\,dt$

where H_n − 1 is the (n − 1)-dimensional Hausdorff measure. In particular, by taking g to be one, this implies

$\int _{\Omega }|\nabla u|=\int _{{-\infty }}^{\infty }H_{{n-1}}(u^{{-1}}(t))\,dt,$

and conversely the latter equality implies the former by standard techniques in Lebesgue integration.

More generally, the coarea formula can be applied to Lipschitz functions u defined in Ω ⊂ Rⁿ, taking on values in R^k where k < n. In this case, the following identity holds

$\int _{\Omega }g(x)|J_{k}u(x)|\,dx=\int _{{{\mathbb {R}}^{k}}}\left(\int _{{u^{{-1}}(t)}}g(x)\,dH_{{n-k}}(x)\right)\,dt$

where J_ku is the k-dimensional Jacobian of u.

Applications

Taking u(x) = |x − x₀| gives the formula for integration in spherical coordinates of an integrable function ƒ:

$\int _{{{\mathbb {R}}^{n}}}f\,dx=\int _{0}^{\infty }\left\{\int _{{\partial B(x_{0};r)}}f\,dS\right\}\,dr.$

Combining the coarea formula with the isoperimetric inequality gives a proof of the Sobolev inequality for W^1,1 with best constant:

$\left(\int _{{{\mathbb {R}}^{n}}}|u|^{{n/(n-1)}}\right)^{{{\frac {n-1}{n}}}}\leq n^{{-1}}\omega _{n}^{{-1/n}}\int _{{{\mathbb {R}}^{n}}}|\nabla u|$

where ω_n is the volume of the unit ball in Rⁿ.

References

Federer, Herbert (1969), Geometric measure theory, Die Grundlehren der mathematischen Wissenschaften, Band 153, New York: Springer-Verlag New York Inc., pp. xiv+676, ISBN 978-3-540-60656-7, MR 0257325 .
Federer, H (1959), "Curvature measures", Transactions of the American Mathematical Society (Transactions of the American Mathematical Society, Vol. 93, No. 3) 93 (3): 418–491, doi:10.2307/1993504, JSTOR 1993504 .
Fleming, WH; Rishel, R (1960), "An integral formula for the total gradient variation" (PDF), Archiv der Mathematik 11 (1): 218–222, doi:10.1007/BF01236935
Malý, J; Swanson, D; Ziemer, W (2002), "The co-area formula for Sobolev mappings" (PDF), Transactions of the American Mathematical Society 355 (2): 477–492, doi:10.1090/S0002-9947-02-03091-X .

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Coarea formula

Applications

See also

References